Fluolab1 光学显微镜原理
1 导言
在本章中，我们将依据几何光学和波动光学的基本原理，系统性地剖析光学显微镜的构造与成像机制。我们的重点是阐述显微镜操作背后的基础物理定律，而非纠结于复杂光学结构的细枝末节，旨在为读者构建一个宏观且扎实的理论框架。核心目标是揭示显微成像技术的能力边界与内在局限，为后续学习更高级的专业知识奠定坚实的基础。
尤为值得一提的是，本章还将介绍生物科学领域中两项至关重要的光学对比技术——相位衬度 (Phase Contrast) 和 微分干涉衬度 (Differential Interference Contrast, DIC)。这两项技术凭借其独特优势，极大地增强了对生物及医学研究中常见的透明样本的观察效果，丰富了我们观察和理解微观世界的视角。相位衬度技术通过巧妙地利用光波穿过样本不同区域时产生的相位变化来创造图像对比度；而DIC技术则更进一步，通过引入微小的光程差，实现了对样本结构更精细的呈现。
此外，本章还详细阐述了荧光显微镜的基本原理、关键组件及其在科学研究中的广泛应用。作为现代生物学研究不可或缺的工具，荧光显微镜利用特定波长的光激发样本中的荧光分子，并通过高灵敏度的探测器捕捉这些荧光信号，从而生成色彩斑斓、信息丰富的图像。我们还将关注荧光显微镜技术的最新进展，包括高分辨率成像方法、多色荧光标记技术以及自动化与智能化操作平台的开发，这些创新正不断推动着生命科学研究向前发展。
2 制造光学显微镜
2.1 光学显微镜的组件
光学显微镜的精密构造依赖于两大核心系统的协同工作：照明系统与成像系统。两者功能不同，却相辅相成，共同决定了显微镜的光学分辨率与图像对比度。初学者往往只关注成像光路上的光学元件，认为它们才是“显微镜的精髓”，却容易忽视照明系统同等重要的作用。事实上，照明与成像通过各自独特的光路设计，共同描绘出微观世界的清晰画卷。
在初步探讨中，我们采用几何光学的基本框架来审视这两大系统，即侧重于光线的传播方向与路径，暂时不考虑光的波动性及复杂的衍射效应。这种简化有助于我们直观地理解显微镜的基础工作机制。然而，必须指出的是，光的波动与衍射现象对显微镜性能的精细调控至关重要，这些更深层次的话题将在本章后续内容中进行全面剖析。
2.2 成像路径
现代显微镜的成像系统，其核心是一个精密的双透镜结构，由物镜 (Objective Lens) 与管镜 (Tube Lens) 构成，两者协作将微小样本清晰成像。在此过程中，样本被精确地放置在物镜的前焦平面上。物镜的关键作用，便是将被测物体的图像投射到无穷远处，这一过程遵循几何成像的基本定律。
如图2.1所示，从物体两端（如轴上点o1及离轴点o2）发出的光线，在物镜的作用下经历了复杂的变换。从o1点发出的光线经过物镜后，被转换为一束平行于光轴的光束；这束光穿过管镜并在其后焦平面上聚焦，形成物体的初步像。对于离轴点o2，其光路可以通过两条特殊光线来追踪：一条是穿过透镜中心、方向不变的光线rc，另一条是平行于光轴入射、汇聚于物镜后焦点的光线rp。这两束光线在物镜和管镜之间的空间中保持平行，该区域被称为无穷远空间，其特点是所有从o2点发出的光线在此空间内都保持相互平行。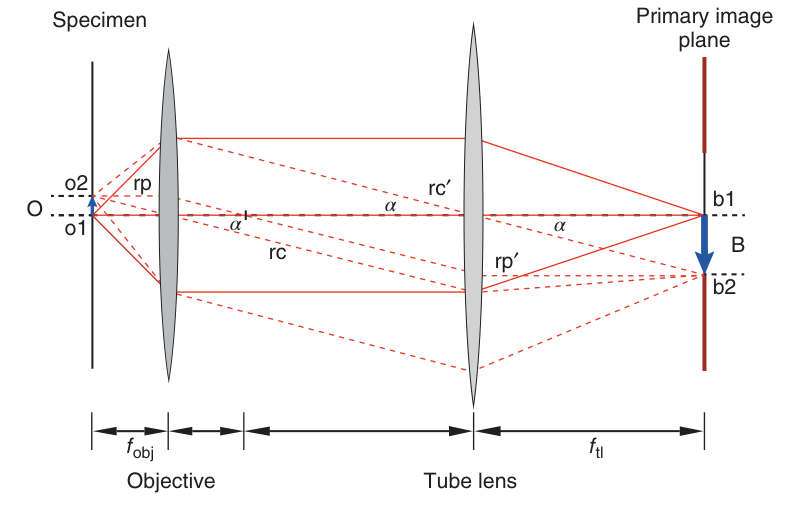 
图 2.1 使用光敏阵列图像探测器的无穷远校正成像过程。 f obj 和 f tl 分别表示物镜和管镜头的焦距。
尽管管镜的位置有一定灵活性，但在实际应用中，为获得最佳成像效果，其前焦点通常与物镜的后焦点重合或非常接近。通过追踪穿过管镜的特殊光线（特别是穿过其前焦点的光线），可以发现这些光线通过管镜后被转换为平行光束rp'，而中心光束rc'则直接穿过，方向不变。这一过程确保了o2点在管镜的后焦平面上准确成像，形成物体的实像，即初级像面 (Primary Image Plane)。像的位置与大小由其与光轴的垂直距离（如b1、b2）决定，从而实现了对物体尺寸的精确放大。
此外，该双透镜系统的放大倍率M是一个关键参数，它直接反映了成像系统对物体尺寸的放大能力。放大倍率M的计算涉及物镜焦距fobj、管镜焦距ftl以及物与像之间的几何关系。
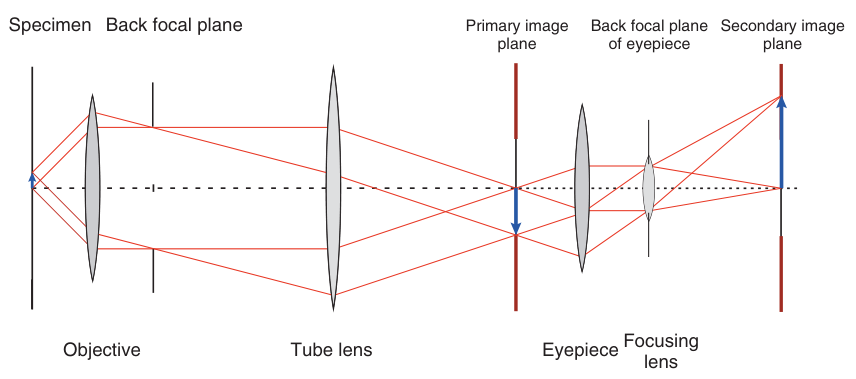
图 2.2 带有两个无限远校正放大级的显微镜。 两个放大阶梯顺序排列的放大系数是两个单一系数的乘积。
为了实现对显微镜样品的清晰观察，显微镜采用了两级放大的设计（如图2.2所示）。第一级放大由物镜和管镜头共同完成，它们协作将样品图像初步放大并形成中间像或主像。物镜的直径通常在2至3厘米之间，其类型和质量直接影响成像的清晰度和分辨率。
第二级放大则是一个与第一级相似的双透镜无限远光学系统，但这次它服务于将中间像进一步放大并投射到观察者的视网膜上。这一级由目镜和眼球透镜组成，共同构成了观察者的视觉接口。视网膜作为第二像面，接收并解析来自显微镜的最终图像。
在显微镜的成像过程中，透镜系统可以通过两种主要方式产生实像：有限光学设置和无限远设置。在有限光学设置中，物体位于透镜的一倍至两倍焦距之间（f < so < 2f），此时透镜在主像面与透镜固定距离上直接形成一个倒立且放大的实像。而在无限远设置中，物体则被放置在物镜的焦平面上，随后利用管镜头等后续光学元件在无穷远处形成图像，这种设置在现代研究用显微镜中尤为常见，被称为无限远校正显微镜。
无限远校正显微镜的优势在于其物镜后的光路中仅包含平行光线，这些光线源自样品的不同位置且相互平行。这一特性使得在物镜与管镜头之间插入额外的平面光学元件成为可能，而不会干扰光束的路径。这些额外的元件，如荧光滤光片立方体、偏振分束器、分析器或附加滤光片等，对于实现各种对比成像技术至关重要。
此外，无限远校正物镜还允许通过移动物镜而非样品台来进行对焦，这一特性在需要精确控制对焦位置或样品位置受限的情况下尤为有用。综上所述，无限远校正显微镜以其灵活的成像配置、高清晰度的成像能力以及便于集成额外光学元件的特点，在科学研究和技术应用中发挥着不可替代的作用。它也可用于补偿残余像差。这种设置的最大优点是物镜后的光路只包含来自不同物体位置的平行光线。由于平行光束只会被平面平行的光学元件位移，因此有足够的空间插入额外的平面光学元件，而不会扭曲光束路径。荧光滤光片立方体、偏振分束器、分析器或附加滤光片等光学元件是各种对比技术所必需的。它们大多安装在物镜和管镜之间。无穷远校正物镜的另一个优点是可以通过移动物镜而不是试样台来对焦。
2.3 放大倍率
在有限光学装置中，尤其是中小倍率的普通透射光显微镜，物镜直接生成实像及倒立的主像，这一技术在商业上具有显著优势。然而，其主要局限在于，即便是平面平行的光学元件插入系统后，也会不可避免地扭曲成像光束的路径。为了纠正这一问题，物镜与主像面之间需增设一套透镜系统。
现代显微系统中，光检测装置如CCD相机常直接安装在主像平面上，简化了成像流程，仅需一步放大即可捕获图像。但在目视观测场景下，主像需通过目镜系统进一步放大，随后置于目镜前焦平面附近，目镜则负责将图像映射至无限远处，便于人眼聚焦于视网膜上，此时眼睛成为成像系统中不可或缺的一环（如图2.2所示）。由于主像位于前焦平面，从目镜出射的光线保持平行，模拟了观察无穷远物体的效果，这是眼睛最为舒适的视觉状态。
目镜在此扮演了放大镜的角色，与眼睛协同工作，形成第二个无限远成像系统，最终将图像清晰投射至视网膜。值得注意的是，图2.2及本章其他图示中，目镜被简化为单透镜，实际上它同物镜一样，是由多个内部透镜精密组合而成的系统，用以校正成像中的各种伪影。
至于目镜的放大倍率（即第二级放大），其计算依赖于放大镜的放大系数，该系数通过比较使用（B'）与不使用（B）放大镜时物体像的大小与原始大小（O）的比值（Mmg = B'/B）来确定。在无穷远系统中，此放大倍数可简化为眼球透镜焦距（feye）与放大镜焦距（fmg）之比（Mis = feye/fmg），进而得出像的大小B' = O × feye/fmg。当物体置于眼睛正常视距（250毫米）处直接观察时，视网膜上像的大小B约为O × deye/250毫米，其中deye为眼球晶状体至视网膜的距离，近似等于眼球焦距feye。由此，可推导出放大镜的放大倍数为Mmg ≈ 250mm/fmg。
最终，将显微镜目镜的放大系数（Mep，以目镜焦距fep表示）与上述放大镜放大倍数相乘，即可得到复式显微镜的总放大倍率：
理论上，总放大倍率可以是无限的；但是，应该选择的有意义的放大倍率是可以明确定义的。最佳放大系数的确定将在第 2.3.6 节中讨论。
2.4 角度和数值孔径
物镜作为显微镜系统的核心组成部分，其一个至关重要的特性在于其收集物体发出光线的能力，这一能力通过物镜能够捕捉到的最大光线角度来量化。具体而言，只有当光线位于一个特定的锥度范围内时，这些光线才能被有效利用以形成清晰、完整的图像。这个锥度范围的最大值，即物镜的总角度开度，也被称作角度孔径，是定义物镜性能的一个关键参数（如图2.3所示）。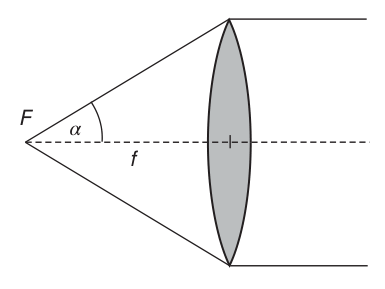 
图2.3 物镜的角度孔径
在图2.3中，角度𝛼被特别标注出来，它实际上是角度孔径的一半。这个角度的正弦值，在显微镜的光学理论中占据着举足轻重的地位，因为它是计算物镜数值孔径（NA）的基础。数值孔径NA，作为衡量物镜光学性能的一个综合指标，其定义为透镜与物体之间介质折射率的乘积与光线最大入射角正弦值的比值。
这里的n，特指透镜与物体之间介质的折射率，它对于确定光线在传播过程中的路径弯曲程度至关重要。
在生物学研究中，生物样本往往被置于特定介质中进行观察，以改善成像质量。例如，常见的缓冲水溶液的折射率约为nw = 1.33，这种环境适用于大多数常规观察。然而，为了进一步提升分辨率和对比度，科学家们还会采用油浸法，即使用折射率更高的油（如noil = 1.518的浸油）作为介质。值得注意的是，不同介质的折射率要求物镜必须进行相应的设计和优化，以确保最佳的成像效果。
数值孔径NA的重要性在于它直接关联到物镜的分辨率、亮度以及景深等多个方面。更高的NA值意味着物镜能够收集到更广泛角度的光线，从而提高了图像的分辨率和清晰度。同时，它还能增加图像的亮度，使得在低光条件下也能获得良好的观察效果。此外，NA还与物镜的景深密切相关，影响着成像过程中焦点深度的变化。因此，在本章的后续内容中，我们将详细探讨NA的各个方面，以及它如何影响显微镜的成像质量和应用范围。
2.5 视野
在主像面上，可观察到的区域受到一个通常位于目镜内部的视场光阑 (Field Stop) 的限制。这个光阑的直径（以毫米为单位）被称为视场数 (Field Number, FN)。根据视场数和物镜的放大倍率 Mobj，可以计算出在样本上能够成像的最大区域直径 Dobj：
显然，成像质量取决于物镜的场性能，即像场周边区域的成像质量。在老式显微镜中，可用视野数最多为 18，而现在平面消色差显微镜的标准视野数为 20，现代平面消色差显微镜的校正最大视野数可达 28。视野性能差的物镜会在图像外围区域产生模糊和色差。
2.6 照明光束路径
光学显微镜的照明系统扮演着至关重要的角色，其重要性不仅限于单纯照亮不发光的标本，而是与成像光学系统并列，共同塑造着对比模式、决定仪器的分辨率，并调控着整体亮度。这一系统包含两大主要的光学配置，各有特色与适用场景。
其一，是较为直接且结构相对简单的照明方式——源聚焦或临界照明，它以其简洁高效的特点，在某些应用场景中发挥着重要作用。
另一方面，更为广泛采用且功能全面的照明配置则是柯勒照明。柯勒照明以其独特的优势，成为光显微镜照明系统中的主流选择，为科学研究与观察提供了更为优越的光学条件。
2.6.1 临界照明和柯勒照明
在光学显微镜的复杂世界里，照明系统作为成像质量的关键因素之一，其设计与配置直接影响了观察结果的细节与清晰度。图2.4a展示了临界照明的光束路径，这是一种基础而直接的照明方式。在此模式下，光源通过聚光透镜（即所谓的聚光器）直接投射到物体平面上，形成一个明亮的照明区域。聚光透镜前焦面上的可变孔径调节着透镜的孔径大小，进而控制照射到试样上的光量，但同时也影响着照明区域的范围。光源的选择至关重要，通常采用乳白玻璃灯泡或背面照射的乳白玻璃板，以确保光源尽可能大且均匀无特征，以避免物体亮度受到不均匀照明的干扰。临界照明因其操作简便、设置直观且所需光学元件少，而广泛应用于不具备特殊对比技术的常规显微镜中。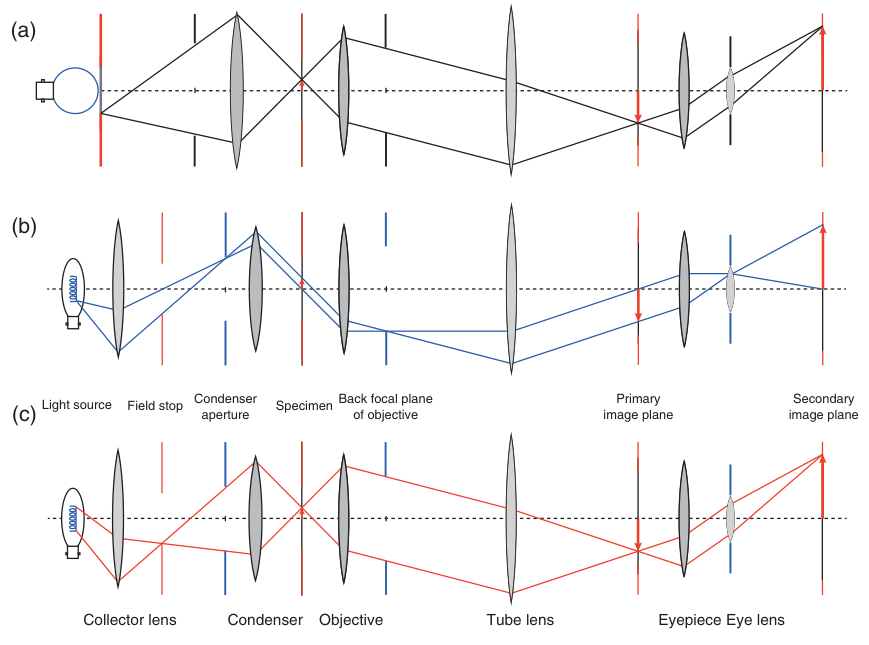 
图 2.4 照明和成像光束路径。(a) 临界照明。(b) 科勒照明和 (c) 相应的成像光束路径。
相比之下，柯勒照明（如图2.4b所示）则是科学显微镜领域的标准照明模式，得名于其发明者奥古斯特-柯勒在1893年的创新贡献。此照明系统复杂而精细，由光源、双光阑（场挡与聚光器孔挡）、双透镜（收集器与聚光器）组成。光源的灯丝经过聚光透镜前焦面的集光透镜成像，确保所有离开聚光镜的光线以平行光束的形式射向物体平面，并通过试样。这一过程中，物镜将未衍射的平行光束聚焦于其后焦平面上，形成光源的像，体现了光学共轭平面的概念。特别地，物镜后焦平面与聚光透镜前焦平面互为共轭，这一特性在相位对比、DIC等高级对比技术中发挥着核心作用。
柯勒照明的优势显著：
照明均匀：即使光源本身不均匀，样本平面也能获得均匀的照明。
独立调节：视场光阑控制照明区域的大小，而孔径光阑控制照明光束的角度（即照明的NA），两者可以独立调节。
灵活控制对比度与分辨率：通过调节孔径光阑，可以在不改变照明区域大小的情况下，精细调控图像的对比度和分辨率。
共轭平面的应用：聚光镜的前焦平面（孔径光阑）与物镜的后焦平面是光学共轭平面。这一特性是实现相位衬度、DIC等高级对比度技术的基础。
综上所述，无论是临界照明还是柯勒照明，它们各自以其独特的方式优化着显微镜的照明效果，为科学研究与观察提供了强有力的支持。而柯勒照明，以其卓越的性能和广泛的应用潜力，已成为现代科学显微镜不可或缺的组成部分。
2.6.2 明视野和落射照明
前面讨论的照明方式，光线都穿过样本再进入物镜，这种配置被称为透射照明 (Transmitted Illumination) 或明场照明 (Bright-field Illumination)。
然而，在许多情况下，从观察的同一侧照亮样本更为有利，例如观察不透明或荧光的样本。这种配置被称为落射照明 (Epi-illumination) 或反射照明 (Reflected Illumination)。如图2.5所示，光源的光线通过一个半透镜 (semi-transparent mirror) 或 分色镜 (dichroic mirror) 被导入物镜，物镜此时既作为成像元件，又充当了聚光镜的角色，将照明光聚焦在样本上。柯勒照明同样可以在落射照明中实现。
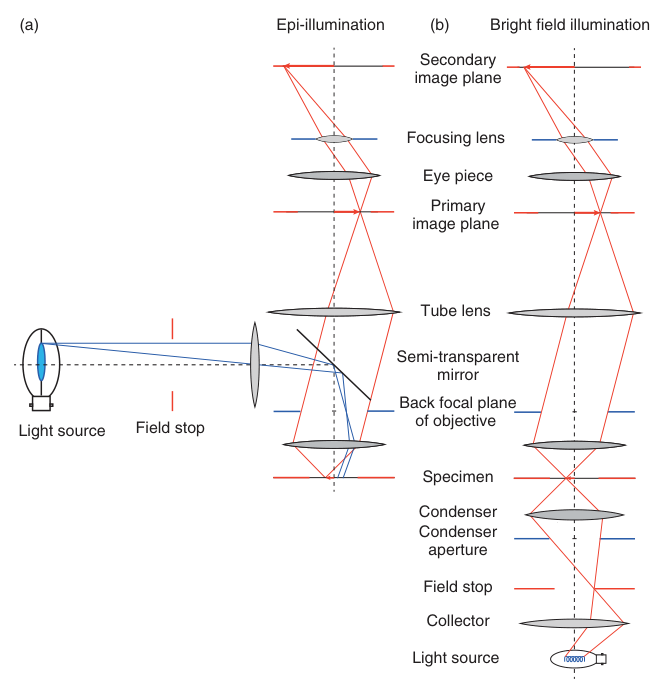
图2.5 显微镜的不同照明方式
根据结构，显微镜可分为正置显微镜 (Upright Microscope) 和倒置显微镜 (Inverted Microscope)。正置显微镜的物镜在样本上方，从上往下观察。倒置显微镜的物镜在样本下方，适用于观察培养皿或细胞培养瓶中的活细胞，便于进行显微注射等操作。
3 波动光学和分辨率
几何光学可以解释放大倍率等基本成像特性，但要理解分辨率的极限，则必须考虑光的波动性。放大倍率 (Magnification) 和 分辨率 (Resolution) 是两个完全不同的概念。我们可以通过增加透镜来轻易提高放大倍率，但分辨率存在一个无法逾越的物理极限。分辨率指的是成像系统区分两个邻近细节的能力。对于光学显微镜，使用绿光和高品质油浸物镜时，这个极限距离约为0.25微米（250纳米）。这意味着我们无法用传统光学显微镜看清活细胞中的单个蛋白质或超分子复合物的细节。在后续章节中，我们将讨论如何通过先进的光学技术来突破这一基本的光学分辨率极限。
3.1 成像过程的波光学描述
根据恩斯特·阿贝（Ernst Abbe）的理论，我们可以严谨地探讨光学分辨率的极限。其核心思想是：当光照射物体时，会发生衍射 (Diffraction)。
假设物体是一个间距为d的精细光栅。当一束波长为λ的平行光垂直照射光栅时，会产生一系列特定角度的衍射光束。这些衍射角αn满足布拉格条件：
这些衍射光束进入物镜后，会在物镜的后焦平面 (Back Focal Plane) 上汇聚成一系列衍射光斑。物镜的后焦平面实际上呈现了物体衍射图样的傅里叶变换。物体的结构越精细（d越小），衍射光斑之间的距离就越远。
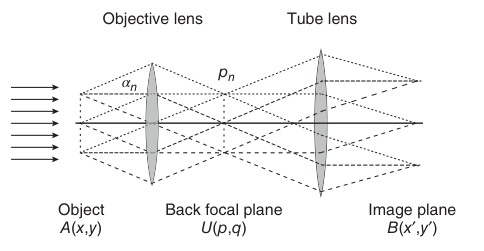
图2.6 光栅结构的成像
最终的图像，是由这些衍射光在像平面上再次干涉 (Interference) 形成的。物镜的孔径是有限的，它只能收集一定角度范围内的衍射光。如果物体的结构过于精细，其高级次的衍射光（甚至一级衍射光）会超出物镜的接收角度而被丢失。当至少0级和±1级衍射光被物镜收集并参与成像时，物体的周期性结构才能被分辨出来。这就是显微镜分辨率极限的物理原因。
考虑到物镜的最大接收角αmax和介质折射率n，对于周期性物体，横向分辨率的极限为：
这个公式表明，要获得更高的分辨率，可以使用更短波长的光（λ更小）或更高数值孔径（NA）的物镜。
3.2 艾里斑模式
之前关于成像光栅结构的讨论揭示了显微镜分辨率极限的物理原因。现在，让我们在物镜前的焦点处放置一个点物体，而不是光栅，如图2.7所示。同时，我们假设光线束与光轴之间的角度很小，并忽略光的矢量特性。点物体会将入射光衍射成球面波wo。球面波的一部分被透镜（假设为理想且无像差的）转换成平行波前wi。如前所述，这种振幅恒定的波前对应于点物体的衍射图像。然而，它受到物镜有限角孔径的修正。根据惠更斯原理，我们可以想象透镜后焦平面上的平行波前wi的每个点都是惠更斯小波的发源地。所有小波都具有相同的相位，因此完全相干。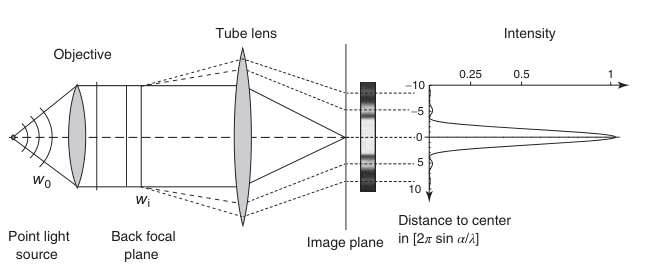 
图2.7 源于物镜出瞳的小波干涉
如果在物镜后放置一个管镜以投射衍射图样，则由于只有该点对所有小波的光程长度相同，小波在像平面上的焦点处会相互产生相长干涉。这一点也对应于点物体的图像位置，可通过几何光学或光线追踪确定。然而，由于这个图像光斑是有限范围内小波干涉过程的结果，因此它有一个有限的直径。在像平面上，光轴一定距离周围存在一个圆形区域，由于小波的光程长度差异（OPDs），它们在此区域产生相消干涉，这在图2.7中用暗条纹表示。在距离焦点更远的地方，我们发现第二个圆，其中大部分小波产生相长干涉。在相消干涉的暗区周围出现了一个亮环（图2.7中用虚线表示）。这个亮环之后又是一个相消干涉的环，接着是相长干涉的环，以此类推。总的来说，小波的干涉过程导致了图2.7右侧所示的强度分布。该图显示了二维旋转对称强度分布的中央截面。这种明暗相间的强度分布也被称为艾里斑模式，中央的亮点是艾里斑。
正如之前讨论光栅时所述，最终图像是由物镜后焦平面上衍射结构中产生的惠更斯小波干涉形成的。因此，由于干涉的原因，点物体的图像不是一个点，而是一个具有特征强度分布的模糊光斑。这个分布被称为成像透镜的点扩散函数（PSF）。其解析推导并不复杂但冗长，这里不做详细讨论。
再次考虑物镜后焦平面上的圆形平面波段，这是物镜孔径限制下点物体的衍射图像。它对应于被一个平面波照亮的半径为a的圆形孔径后面的场。对于成像过程，只有远离孔径的场才是相关的。因此，我们可以忽略出射波的曲率，只考虑平面波（图2.8a）。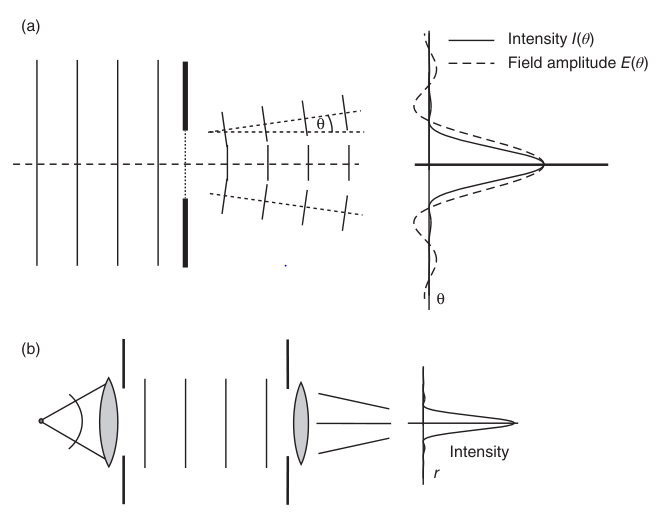 
图2.8 弗劳恩霍夫衍射
为了计算远场，我们需要对孔径处产生的小波贡献进行积分，并计算总场。该情况具有径向对称性，场强仅是光轴角度θ的函数。对于R ≫ a，孔径表面上小波的积分得到以下场E(θ)的表达式：
其中，表示一阶第一类贝塞尔函数。管镜会将这个弗劳恩霍衍射图样从远场投射到其焦平面上（图2.8b）。以角度θ平行落在透镜上的光线在焦平面上距离光轴r处聚焦，其中β是管镜开口角的一半。当我们考虑到管镜的焦距在实际中在160到250毫米之间，镜头孔径最大为20毫米，最大图像尺寸为28毫米时，方程（2.7）中的近似对于管镜是合理的。
将此表达式代入方程（2.6），得到管镜焦平面上场的振幅作为到光轴距离r的函数：
透镜焦平面上作为到光轴距离函数的光强度I(r)通过计算I(r) = [E(r)]²得到。这导致以下表达式（2.9）：
其中I0是透镜焦点的光强度。函数E(r)和I(r)在图2.9中绘制。
3.3 点扩散函数与光学传递函数
前面的讨论直接引出了成像的核心概念，像显微镜这样的光学系统实际上只是物体空间频率的低通滤波器。由于点对象被成像为艾里斑图样，因此精细的物体细节会变得模糊。微观成像实际上是对现实进行平滑处理的过程。
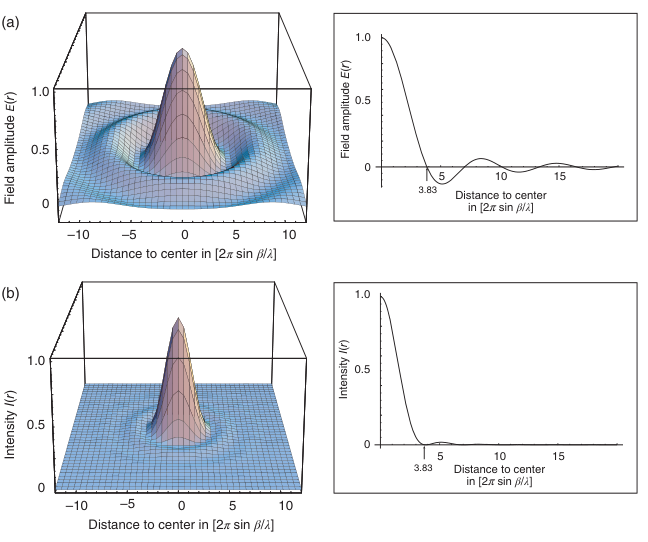
图2.9 对自发光点物体成像时，管状透镜焦平面上的强度和场分布
3.4 横向分辨率与轴向分辨率
3.4.1 使用非相干光源的横向分辨率
透镜系统孔径的衍射是光学成像分辨率限制的原因。一个发光点对象的图像对应于强度分布I(r)（方程(2.9)和图2.9b），这被称为艾里图样。在该图样中，由中心最大值与第一个零点之间的距离定义的圆形区域被称为艾里斑。贝塞尔函数的零点位于x=3.83处，因此，在像平面上艾里斑的半径rim,0由以下公式(2.10)给出：
在像平面上，完整分布的总光量的84%位于距离0 < r < rim,0的范围内。为了找出在物平面上对应的距离robj,0，方程(2.27)必须除以放大因子M。rim,0在物空间中的对应值为robj,0 = rim,0/M。考虑到物镜/管镜系统的正弦条件，并考虑到物空间中通常存在折射率为n的浸没介质，需要使用𝜆/n作为波长，我们得到robj,0的表达式为(2.11)：
其中𝛼表示物镜开角的一半。注意n sin 𝛼是物镜的数值孔径（NA）。而将2.11带入到2.10则可以得到robj,0的公式（2.12）
现在，我们来看由两个相距d的相邻点对象产生的图像。首先，我们考虑非相干光源，例如两个单独的荧光分子。由于发射体彼此独立，它们的光不能相互干涉。这两个点对象不是以点的形式成像，而是以“模糊”的强度分布形式成像，如图2.10所示。总的光分布是通过将方程(2.9)给出的两个强度分布相加得到的。当d > robj,0时，仍然可以观察到两个明显分开的最大值（图2.10a）。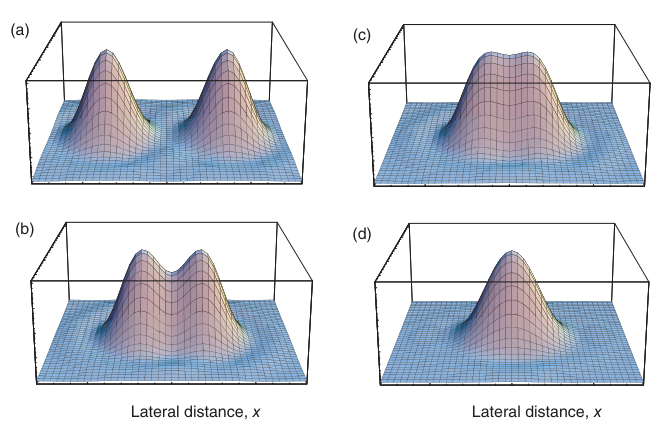 
图2.10 两个非相干点光源在图像平面上的强度分布表面图。
如果点对象在物空间中以距离d靠近彼此，且d = robj,0，则它们的艾里斑在像平面上会明显重叠（图2.10b）。在这种情况下，两个最大值中心之间的信号强度约为最大强度的75%。我们说两个对象是可分辨的，当它们在图像中仍然可以相互区分时。分辨率丧失的确切距离取决于探测器或观察者区分强度水平和信噪比的能力（图2.10c）。因此，分辨率距离的确切定义有些任意。瑞利勋爵提出距离d = robj,0作为光学分辨率的判据，因为在这种情况下，人眼仍然可以感知到两个分开的图像点。这一条件被称为瑞利判据。如果对象之间的距离远小于该值，则它们无法再被感知为单独的对象（图2.10d）。根据瑞利判据，光学分辨率dR为：
dR越小，光学系统的分辨能力越高。该公式解释了为什么使用短波长的光（如蓝色甚至紫外线）相比长波长的光（如红色或红外线）能提供更高的分辨率。结合使用高NA物镜和具有更高折射率（如水、甘油或油）的浸没介质以及合适的物镜，可以进一步提高分辨率。
3.4.2 相干光源的横向分辨率
对于两个相干点光源，情况则有所不同。这些光源可能由显微镜样品同一平面上的两个小结构形成，它们被平面波照亮。随后，两个光源发出的衍射光波具有相同的相位，并可能在像平面上相互干涉，最终形成的场分布由两个场分布之和决定，如方程(2.8)所示（见图2.9a）。观察到的光强度分布现在是通过场贡献之和的平方得到的，而不是像之前讨论的自发光点对象那样通过各个场贡献的平方和得到。这产生了与不相干点对象截然不同的图像，如图2.11所示。在图2.11中，展示了两个相干点光源的图像，它们在物平面上彼此相距d。这个图像与不相干情况（图2.10）大相径庭。特别是，当d等于方程(2.13)中定义的robj,0时，两个像点显然是不可分辨的。相反，需要更大的距离d，使得两个最大值之间的光强达到约0.75I0的最小值。这个值可以用作两个相干点光源的“瑞利型”分辨率极限。显然，相干对象的光学分辨率降低了2倍。这是一个重要事实，因为相干对象在显微成像中很常见。在明场照明中关闭聚光镜光圈会产生点状光源。通过样品的光是相干的，因此衍射波也是相干的。在这种情况下，横向分辨率由方程(2.14)给出。
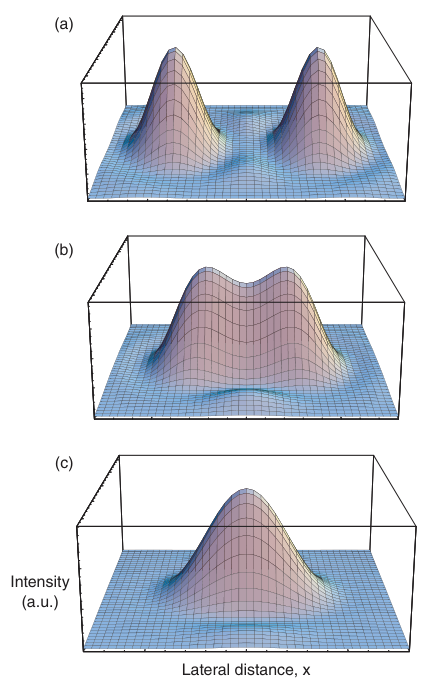
图2.11 两个相干点光源在图像平面上的强度分布表面图。
到目前为止，我们假设照明波沿光轴传播并同时击中物平面上的结构。在这种情况下，衍射波之间没有相位差。然而，当入射波与光轴成一定角度传播时，情况就大不相同了。此时，起源于物平面的惠更斯衍射小波相对于彼此具有特定的相位差，因为它们是根据在样品中的位置在不同时间点产生的。这种衍射光中的相位差在光被聚焦的像平面上仍然存在，图像由相干且相位偏移的波的干涉形成。现在，必须像之前那样对两个场振幅进行求和，但必须考虑它们之间的相对相位差。当样品被扩展光源的透射光照亮时（例如，通过完全打开的聚光镜光圈），则存在许多不同的照明点光源。当接近光圈极限时，这些光源的照明角度各不相同。每个光源本身都会照亮样品并产生来自样品的相干衍射光。然而，就彼此而言，这些光源是不相干的，因为它们对应于照明灯丝上的不同位置，因此在像平面上产生的所有光分布必须一起求和。必须在各个斜照明角度产生的强度分布上以适当的方式进行求和。必须考虑到，由于聚光镜外圈中更斜的照明方向数量更多，因此它们的贡献更大。最终图像取决于照明的详细模式，或者换句话说，取决于照明光的相干程度，这可以通过聚光镜光圈的大小来调节。确切地说，是聚光镜照明的数值孔径（NAcond）决定了照明光的相干程度。根据瑞利判据，最终分辨率可以表述如下：
对于带有聚光镜的明场照明，可实现的分辨率取决于照明透镜的性质及其数值孔径（NA）。关闭聚光镜光圈（减少样品中的光散射）会降低可获得的光学分辨率，因为照明光的整体相干性增加了。必须在减少杂散光和提高焦深之间，以及降低横向光学分辨率之间做出选择。
3.4.3 轴向分辨率
截至目前，我们讨论了图像平面内光强的精确分布。然而，图像形成是一个三维过程。光波通过物镜前方的空间（即物空间）、物镜、物镜与管镜之间的空间以及管镜，最终到达图像平面。随后，这些光波在图像空间内聚焦形成图像。它们不仅在图像平面内相互干涉，还填充了管镜之后的所有空间，产生了复杂的三维光强分布。艾里斑（Airy pattern）精确地描述了初级图像平面内的横向光强分布。其数学表达式（方程（2.9）可以通过所谓的近轴近似进行解析推导。这意味着它仅在接近物体和图像空间光轴的小区域内有效，且所考虑的光轴角度必须很小。利用近轴理论，可以解析地计算出自发光点图像中心附近完整的三维光强分布。图2.12展示了这一分布的图形表示，该分布以归一化光学单位表示到图像中心的距离的函数。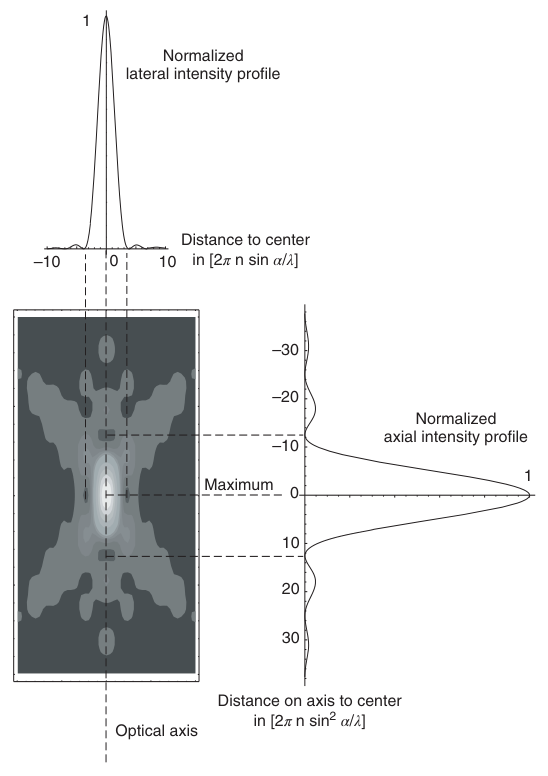 
图2.12 根据准轴向理论得出的三维光强分布。
沿光轴的光强分布可以进行解析描述，光轴上强度最大值与第一个最小值之间的距离z0,im可以作为轴向分辨率的判据，类似于瑞利判据。在图像空间中，对于低数值孔径（NAobj）的情况，z0,im由下式给出：
由于，这对应于物空间中的轴向距离z0,obj：
实际上，这是自发光点物体所在物体台必须移动的垂直距离，以使图像从中央强度最大值变为第一个最小值。虽然横向分辨率取决于NA的倒数，但轴向分辨率与NA²的倒数相关。图2.13展示了不同浸没介质下横向和轴向分辨率对NA的依赖关系。确实，在相同的NA下，水浸和空气浸物镜比油浸物镜具有更高的轴向分辨率，但它们的径向分辨率没有差异。
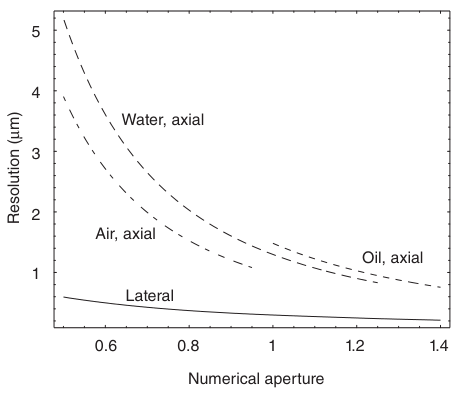
图2.13 空气、水和油浸物镜的轴向和横向分辨率与数值孔径的函数关系。
3.5 放大和分辨率
在深入探讨显微镜成像技术时，我们首先要认识到点状物体在图像平面上的横向表示与著名的艾里模式（Airy pattern）紧密相关。这一模式不仅揭示了光的衍射效应，还直接关联到显微镜的分辨率极限。在现代显微成像系统中，图像通常由高灵敏度的数字设备如CCD摄像机捕获，这些设备具备特定尺寸的探测器元件（通常表示为dd）。
为了最大化显微镜的分辨率潜力，选择适当的整体放大倍率至关重要。理想情况下，这一放大倍率应确保图像平面上的艾里斑半径（dAiry）至少为探测器元件尺寸（dd）的两倍。如图2.14所示，当探测器元件尺寸接近艾里斑半径的一半（dd ≈ dAiry/2）时，图像探测器能够最有效地捕捉并记录图像中的所有可用信息，从而避免信息丢失或模糊。
因此，确定最佳放大倍率（Mopt,d）需综合考虑光学系统的分辨能力以及检测系统的特性，特别是探测器元件的尺寸，如CCD光电二极管的边长。根据这一逻辑，最佳放大倍率可近似等同于光学系统可达到的分辨率（dR），这一关系在公式(2.12)中得到了定义。
以横向光学分辨率为0.25微米的显微镜和探测器尺寸为6.25微米的场景为例，计算得出的最佳放大倍率应不低于50倍。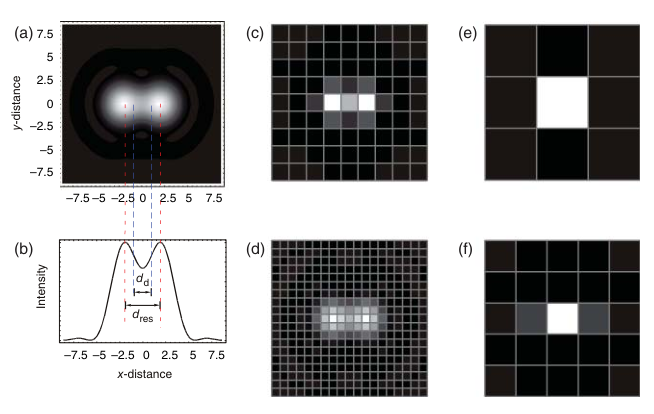 
图2.14 光学分辨率和探测器元件尺寸。 (a) 以瑞利距离 dres 分隔的两个点物体的图像。(b) 通过图像水平中心的线剖面图。(c) 使用探测器元件尺寸 dd = M × dres/2 生成的图像。M 是整体放大系数。在数字化图像中，两个物体被分开。(d) 探测器尺寸 dd = M × 0.24 × dres。可以识别两个物体的强度分布细节。这种情况被称为 "超分辨率"。如果 dd > M × dres/2，数字化图像将无法保持光学分辨率，如 (e) dd = 1.5 × M × dres 和 (f) dd = 0.9 × M × dres 所示。
然而，当考虑显微图像的视觉检测时，情况则有所不同。人眼的分辨率受限于能够区分两个物体点的最小视觉开角，这一角度通常不小于2或弧度。若将0.25微米的物体置于25厘米的舒适视距处，其对应的视角仅为弧度，远低于人眼的分辨极限。
为了满足目视观察的需求，总放大倍率（Meye）需显著增加。这一放大倍率通常通过多级放大系统实现，其中第一级由物镜和管状透镜组成，提供初步放大（如100倍），第二级则由目镜和眼睛共同完成进一步放大（如10倍）。这样的组合确保了图像在视觉上足够清晰，便于观察和分析。
值得注意的是，超过公式(2.18)和(2.19)所定义的最大有效放大倍率的额外放大被称为“空放大倍率”，因为它不再提供新的图像信息，而是简单地放大了已存在的图像细节，可能导致图像质量的下降或观察的不便。因此，在实际应用中，合理控制放大倍率是实现高质量显微成像的关键。
3.6 景深和焦深
在光学成像系统中，景深（Depth of Field, DoF）和焦深（Depth of Focus, DoF）是两个关键概念，它们分别描述了物体空间和图像空间中能够保持图像清晰度的范围。理解这两个概念对于优化成像系统的性能以及获得高质量的图像具有重要意义。
景深是指在物体空间中，沿光轴方向能够保持图像清晰度的最大距离范围。它反映了成像系统对轴向位置变化的敏感程度。具体来说，景深定义了在不显著降低图像清晰度的情况下，薄物体能够沿光轴移动的最大距离。景深的大小受多个因素影响，其中最重要的两个因素是物镜的数值孔径（NA）和成像介质的折射率。数值孔径越大，系统收集光线的能力越强，但对轴向位置的变化也更加敏感，从而导致景深减小。此外，介质的折射率通过影响光在介质中的传播速度，间接地影响景深的大小。在实际应用中，景深的计算通常基于特定的公式，例如公式(2.17)，而其具体数值通常为该公式计算结果的两倍，以确保评估的准确性和实用性。
与景深相对应的概念是焦深，它描述的是在图像空间中与景深相对应的距离范围。焦深与景深之间存在一定的数学关系，即焦深等于景深乘以放大系数M的平方。这一关系表明，焦深的大小不仅取决于景深，还受到系统放大倍数的影响。在实际应用中，显微镜等成像系统通常采用较大的放大倍数以获得更精细的图像细节。例如，在放大100倍的情况下，焦深可能达到几毫米的量级。这一较大的焦深范围确保了即使在成像系统存在微小轴向偏差的情况下，仍能保持图像的清晰度和分辨率。
总的来说，景深和焦深是光学成像系统中不可忽视的重要参数。景深决定了物体空间中能够清晰成像的范围，而焦深则确保了图像空间中清晰度的稳定性。通过合理设计和调整光学系统的参数，如数值孔径、介质折射率和放大倍数，可以有效控制景深和焦深，从而满足不同应用场景下的成像需求。例如，在显微镜成像中，较大的焦深能够帮助研究人员在观察微小结构时保持图像的清晰度，而在摄影领域，控制景深则能够实现背景虚化或全景清晰的效果。因此，深入理解景深和焦深的概念及其影响因素，对于优化成像系统的性能具有重要意义。
3.7 超采样和欠采样
在探讨成像技术的广泛应用时，我们不可避免地会遇到对图像分辨率需求的多样性。在某些特定的成像场景下，追求远超最优放大系数（Mopt）的放大级别变得尤为关键，这一做法被业界称为“超采样”。超采样的核心目的并非直接挑战光学成像系统的固有分辨率极限，因为从物理原理上讲，光学成像无法揭示超出其光学分辨率的精细结构信息。然而，通过超采样技术，我们能够以极高的精度定位那些尺寸远小于分辨率极限的微小物体，如单个分子，这对于生物、材料科学等领域的研究具有重大意义。
为了实现这一目标，关键在于获取完整且高分辨率的点扩散函数（PSF）图像。在超分辨率成像的实践中，通常采用一种精细的采样策略，即在每个方向上使用3到7个像素对衍射极限信号进行详尽的采样。这种策略确保了即使在极端放大条件下，也能捕捉到足够的细节信息，为后续的数据处理和图像重建提供坚实的基础（详细技术细节可参见第8章和第12章）。
另一方面，成像技术的应用并非总是追求极致的分辨率。在某些实验或应用场景中，研究者可能仅需对特定视场内的物体进行计数或粗略的形态分析，如细胞数量的统计。在这种情况下，高分辨率成像不仅不是必需的，反而可能增加数据处理的复杂性和时间成本。此时，采用相对粗糙的成像策略，即所谓的“欠采样”，便成为了一种高效且实用的选择。欠采样通过减少图像中的像素数量或降低采样频率，实现了在保证基本信息不失真的前提下，大幅度提升成像速度和降低数据处理难度的目标。
4 2.4 孔径、瞳孔和远心
在深入探讨光学显微镜的高级特性时，我们不仅要关注其生成标本放大图像的基本能力，还需细致理解图像质量提升背后所涉及的光学原理与系统设计。显微镜，作为高度复杂的光学系统，其性能受限于多个关键因素，特别是光波在通过多个放大级和可能的中继级后如何精准地抵达图像平面。
首先，我们必须认识到透镜收集光量的物理限制，这主要由透镜的物理直径即“孔径”决定。这些孔径不仅影响着光波的通过量，还直接关系到成像的亮度和质量。值得注意的是，光圈的大小并不直接关联于镜头的焦距，后者更多地决定了成像的放大倍率。在简单的透镜系统中，边缘或安装位置定义了“入口孔径”，它初步限定了可进入成像系统的光量。而在更复杂的物镜系统中，通常由最小透镜的直径或附加的可调光圈挡板来精确控制光束的横向传播。
对于显微镜而言，入口瞳孔（从物体同轴点看到的孔径图像）和出口瞳孔（从图像同轴点看到的极限光圈）的位置至关重要。当光圈挡板位于物镜后焦平面时，这一结构具有显著优势：它使得入口瞳孔看似位于无限远处，从而确保主光线平行于物体空间的光轴，形成所谓的远心透镜效应。这种设计带来的核心优势在于，即便物体发生散焦，图像在像面上的模糊程度会增加，但放大倍率却能保持不变，这对于显微镜的稳定操作和精确测量至关重要。
图 2.15 物镜的光阑和出瞳。（a）光阑位于透镜的前方，因此与入瞳相同。出瞳是从图像的轴上点观察到的光阑的虚像（注意从该点到光阑图像的黑色虚线）。（b）物镜的光阑和出瞳位于其后焦平面。这导致入瞳位于像空间的无穷远处。此外，在柯勒照明中，聚光镜的入瞳和物镜的出瞳彼此共轭。
在透射显微镜中，柯勒照明模式因其照明均匀性和可控性而广泛应用。此模式下，照明系统的入口瞳孔由聚光镜孔径实现，其位置恰好在聚光镜的前焦平面，该平面同时也包含了成像系统的出瞳。为确保最佳成像效果，这两个瞳孔的大小应保持一致，以充分利用照明光并减少光损失。此外，固定入口和出口瞳孔的位置（即无穷远或物镜后焦平面）在物镜切换时显得尤为重要，因为它避免了聚光镜的轴向重新定位，简化了操作流程。
图 2.16 远心性。(a) 带有孔径光阑（即物方入射光瞳）的透镜的成像过程。主光线是从最外侧物体位置（黑色箭头的尖端）穿过孔径中心的射线。主光线代表形成该点图像的光锥，其在像空间的路径标示着离焦图像的中心。在示意图中，主光线是红色的中心光线。(b) 当物体离焦时，与 (a) 中的位置相比，主光线在固定的像平面上向下移动，如箭头所示。(c) 物方远心透镜的成像过程。根据此类透镜的定义，孔径光阑位于后焦平面上。现在，主光线穿过后焦点，并在物方平行于光轴。(d) 对于远心透镜，物体离焦不会改变主光线的位置，因为它始终平行于光轴。它在像平面上与 (c) 中相同的位置相交（参见 (c) 和 (d) 中红色箭头的位置）。
特别在荧光显微镜等采用落射照明的装置中，照明光路与成像光路的瞳孔位置高度重合，均位于物镜后焦平面，这不仅简化了系统设计，还确保了光路的精确匹配和高效利用。这一设计也为多种透射光对比技术提供了便利，如将在后续章节中详细探讨的几种重要技术。
5 物镜
物镜，作为显微镜的核心与灵魂，其设计与制造融合了高度精密的光学与机械工程技术。一个优质的物镜通常由多达二十个精心挑选的单凸透镜和凹透镜组成，这些透镜各自拥有独特的曲率半径，旨在通过复杂的光学组合实现最佳成像性能。为了消除像差、确保图像质量，这些透镜的安装精度需达到极高的标准，这一要求在高端物镜中尤为严苛，而对于那些配备可移动透镜组及校正环的物镜而言，更是至关重要。因此，物镜的设计不仅是对光学原理的深刻理解与应用，更离不开精密机械技术的支持，二者相辅相成，共同铸就了显微镜成像的基石。
物镜的主要功能在于捕捉并汇聚来自被观察物体的光线，随后与显微镜的管透镜协同工作，共同形成清晰、准确的主实像。这一过程要求物镜不仅能够有效抑制各种像差，如球差、色差等，还需具备高分辨率，以呈现物体的细微结构与细节。此外，物镜还承担着调节显微镜放大倍率、塑造特定图像对比度的重任，是实现高质量显微观察不可或缺的关键部件。
随着科技的进步与应用的拓展，物镜的种类日益繁多，性能各异，以满足不同领域、不同样本的观测需求。从生物学的细胞观察到材料科学的微观结构分析，再到地质学的矿物鉴定，每一种物镜都承载着特定的使命与期望。因此，在选择物镜时，必须充分考虑样本的特性、观测目的以及显微镜的整体配置，以确保获得最为满意的成像效果。
5.1 物镜设计
物镜，作为显微镜成像质量的核心决定因素，其性能直接关联到观测结果的精确性与清晰度。然而，理想图像的形成并非无懈可击，它常受到单色像差与色差的双重挑战。单色像差源于大多数镜头采用的球面设计，而色差则根植于透明介质折射率随波长变化的物理特性中，难以彻底消除。像差的类型与程度深受物场尺寸、焦距、放大倍数、以及入射光束的宽度与倾斜度等因素的影响。
图 2.17 物镜系统。 现代物镜是光学和精密机械工程的杰作。 图中展示的是一个 63×/1.2 NA C-Apochromat 物镜。 这种物镜经过复消色差校正，范围从紫外到可见光，再到近红外光谱范围。 它具有校正环，用于补偿盖玻片厚度和/或样品内折射率的差异。 特定光线的路径和其他详细信息如图 2.18 所示。
为应对这些自然产生的像差，光学工程师们巧妙地将具有不同色散特性、曲率半径、厚度及透镜元件间距的多种玻璃材料组合起来，构建出复杂的透镜系统。这一策略旨在通过精细的参数调整，最大限度地减少或消除各类像差。例如，轴向色差可通过结合两种不同色散特性的玻璃镜片来校正，尽管这种方法可能导致非选定颜色存在轻微偏差，即所谓的二次光谱。
物镜的设计过程既是一门科学，也是一门艺术，它要求设计者具备深厚的光学知识、敏锐的直觉与丰富的经验。设计的起点是明确物镜的各项关键性能指标，如放大倍率、视场数、数值孔径（NA）、工作波长区域、浸入介质、工作距离（WD）以及所需的像差校正水平。随后，设计者需参考既有设计或进行全新创作，精心布局每个透镜元件的位置、选择合适的折射率与材料，这一过程既充满创造力，也极具挑战性，往往耗时数周乃至数月。
为了精确评估与优化透镜系统的成像特性，计算机光线追踪技术成为现代光学设计不可或缺的工具。该技术通过模拟光线在透镜系统中的传播路径，能够直观展现成像过程中的像差表现。设计师需不断调整透镜参数或引入新元件，以逐步逼近理想成像状态。特别是对于显微镜物镜而言，球差与色差的校正至关重要，需严格控制在分辨率极限以内。
图 2.18 物镜像差的校正。(a) 五种不同的 63× 物镜系统的光学设计。从左到右：N-Achroplan，数值孔径0.85，空气浸镜；Plan-Neofluar，数值孔径1.25，油浸镜；Plan-Apochromat，数值孔径1.4，油浸镜；C-Apochromat，数值孔径1.2，水浸镜；以及 Alpha Plan-Apochromat，数值孔径1.46，油浸镜。不同的颜色标记着从焦平面不同位置发出的光束。(b) 对比 (a) 中所示物镜的校正程度，以物镜出瞳处光程差的均方根偏差 (rms-OPD) 作为函数，绘制随波长变化的曲线。N-Achroplan 设计最简单，为消色差物镜；Plan-Neofluar 针对荧光应用进行了优化，在可见光波长范围内表现出良好的色差校正；而 Plan-Apochromat 则表现出卓越的色差校正和极低的场曲。C-Apochromat 在近紫外到近红外光谱范围内具有出色的色差校正，并表现出特别低的场曲。Alpha Plan-Apochromat 具有特别大的数值孔径以及非常好的色差和像面校正。
图2.18生动展示了五种不同63倍物镜的设计实例，从N-Achroplan到Alpha Plan-Apochromat，其像差校正水平逐步提升，体现了设计复杂度的增加与成像质量的显著改善。其中，C-Apochromat以其高NA值与卓越的成像性能脱颖而出，而Alpha Plan-Apochromat则通过牺牲部分成像质量，实现了NA值高达1.46的极端设计，专为全内反射荧光显微镜等高端应用量身定制。
为了定量评估与比较不同物镜的校正水平，均方根光路长度差（rms-OPD）作为一种通用且有效的测量方法被广泛采用。它通过对光线追踪结果进行统计分析，量化了透镜系统在不同波长下的残余像差，为物镜性能的客观评价提供了科学依据。图2.18b的rms-OPD曲线清晰展示了各透镜系统从近紫外到近红外光谱范围内的校正效果，进一步验证了设计优化的必要性与重要性。
最终，值得注意的是，尽管所有物镜设计均力求完美，但实际应用中仍需考虑残余像差与衍射极限之间的平衡。在视觉观测领域，当像差影响低于衍射极限时，其影响可视为可忽略不计；然而，在超分辨率显微镜等高精度成像任务中，任何微小的像差都可能成为决定性因素。因此，对物镜进行细致的测试与比较，确保其满足特定成像需求，是确保观测结果准确可靠的关键所在。
5.2 2.5.2 光收集效率与图像亮度
我们在前面已经看到，由于物镜的开口角度有限，任何物镜都只能捕捉到物体发射或衍射的部分基本波。这就导致光学系统的分辨率有限。此外，它还限制了物镜的集光效率，而集光效率当然是每台显微镜的核心特征。最终，它决定了最终图像的亮度。令人惊讶的是，众所周知，图像亮度与物镜的 NA 值有关，即与物镜开角 𝛼 的正弦值有关，而与物镜的开实角无关。这是第一个直观的猜测。那么，这是真的吗？仔细研究这个问题就会发现其中的原因，同时也会引出显微镜中的一个重要概念，即所谓的正弦条件。首先，我们考虑一个向周围空间发光的点状物体。
图 2.19 物镜的光效。(a) 发光点状物体的成像。(b) 发光二维物体（朗伯辐射源）的成像。
如图 2.19a 所示，透镜收集到的光通量与填充透镜开口的球面段表面成正比，或者用数学术语来说，与开口实角成正比。考虑到围绕光轴的旋转对称性（可用角度 𝜑 标记），我们可以通过对所有表面元素 dS = d𝜙 sin d𝜃 进行积分，计算出表面段的总实体角，计算公式为
可以直接进行积分，因为点物体的光线垂直落在所有表面元素上，而与它们在空间中的位置无关，这就是角度 𝜑 和 𝜃 的特点。因此，物镜在检查点物体时的集光效率与镜头开角的正弦和 NA 值无关，而是由公式 (2.20) 得出。但是，在拍摄二维扩展发光物体时，情况就不同了。现在我们必须确定由表面元素 dA 发出并被透镜收集的光量。这样的发光表面被称为朗伯辐射体。然而，在不同的角度 𝜃 下，dA 的有效可见表面是不同的（图 2.19b）。随着角度 𝜃 的增大，有效可视面会变小，直到假设 𝜃 = 90∘ 时为 0。从数学角度讲，我们现在必须考虑标量乘积 。这会增加一个 cos 𝜃 的因子。如果我们考虑到这一点，并对球面段的总表面进行积分，就会发现
我们注意到，收集到的光通量与发射面元件的尺寸 dA 和物镜开口角正弦的平方有关。这个表达式适用于空气浸入式物镜。如果透镜前方是折射率较高的材料，如水或油，则必须使用适当的浸入式透镜。这种情况如图 2.20 所示。
图 2.20：有浸没介质和无浸没介质时的光通量。
我们可以看到，在折射率为 n 的材料中，以最大角度 𝛼 进入透镜的光通量与在空气中工作时被角度 𝛼 包围的光通量相同。根据折射定律，sin 𝛼 = n sin 𝛼。然而，光通量不会发生变化。因此，在使用光学密度较高的材料时，我们必须用开口角的正弦乘以折射率，才能得到所收集光通量的正确表达式：
因此，我们可以看到，如果成像的是平面二维试样，物镜收集到的光量与其 NA 的平方成正比。当然，这在显微镜下是最常见的情况。
作为开口角 𝛼 和 NA 的函数。在这两种情况下，使用高 NA 镜头的重要性显而易见，尤其是在对点状物体成像时。收集到的光线通过物镜的出瞳后投射到像面上。图像亮度与放大倍率有何关系？当考虑二维自发光物体的图像时，这一点就变得很明显了：放大倍率的增加会放大图像，但由于图像的总综合光度保持不变，其光密度的降低与放大倍率的平方成正比。综合前面的考虑，我们发现图像亮度 B 与 NA 的平方成正比，与放大倍率的平方成反比：
显然，这些考虑忽略了组成物镜的透镜的吸收和反射效应，或特殊透镜的特性，例如相衬物镜中的吸收环。因此，具有相同放大倍率和 NA 的物镜所产生的图像亮度值可能大相径庭。最后需要指出的是，NA 在荧光显微镜中的影响更为显著。在这种情况下，照明是通过物镜实现的，这就在样品平面的辐照度中引入了更多的 NA2 因子。因此，最终图像的亮度与所使用的 NA 值有关。不过，在荧光成像中，亮度与放大倍率的关系消失了，因为放大倍率对照明和成像的影响相互抵消。
5.3 物镜分类
我们已经看到，物镜的一个非常重要的特征是其像差校正程度。在单色像差中，有两种像差，即球差和彗差，在现代物镜中具有衍射限制校正功能，这意味着这些像差低于所有类型物镜的可见度阈值。景差和色差仍然是最重要的像差，物镜根据这些像差的校正程度进行分类。物镜类别名称的第一部分指的是景物曲率的校正程度，第二部分指的是色差的校正程度。对于景物曲率和畸变特别小的镜头等级，会加上一个 "平面 "名称。这类物镜的像场大，图像校正效果好。横向和纵向色差对获得良好的明视野对比度尤为重要，因为当这些色差存在时，物体成像会出现彩色条纹。关于色差校正，显微镜物镜可分为消色差、半消色差或萤石色差和变色差。这些规格都刻在物镜镜筒上。只有消色差物镜通常不标消色差。遗憾的是，每个制造商都以不同的方式标示其物镜，因此很难进行区分和比较。尽管如此，物镜的名称还是表明了其校正程度。除了校正等级外，物镜上还刻有其他重要参数的色标或缩写（表 2.1）。这些参数表示放大倍数、浸入介质和特殊成像应用的适用性。此外，一个或有时两个色环表示可达到的放大倍率和所需的浸入介质（表 2.2 和 2.3）。
表2.1 物镜镜筒上的文字意义
| Position/type | Abbreviation | Meaning |
|---|---|---|
| 图像曲率校正 | - | 低级图像曲率校正 |
| NPL, N plan | 正常视场平面（20 毫米） | |
| PL, plan, plano | 平面视场（25 毫米） | |
| 纵向色度校正 | - | 消色差（低级色度校正） |
| FL, fluotar, neofluar, fluor, neofluor | 荧光或半复消色差 | |
| 放大倍数 | 2.5–160 | 与适当的管状镜头配合使用时，主像面的放大率 |
| 数值孔径 | 0.1–1.46 | 如果给出了一个范围（如 1.25-0.65），则物镜内置了一个可调光圈 |
| 浸入式 | - | 空气 |
| Water, W, W.I. | 水浸 | |
| GLY, Gly | 甘油浸 | |
| Oil, HI, H | 油浸 | |
| IMM | 可用于空气、水或油浸（旧式） | |
| LCI | 可与多种介质配合使用，例如甘油、水或油浸泡介质 | |
| 机械管长度 | ∞ | 无限远机械筒长 |
| 160–250 | 管长（毫米） | |
| 盖板玻璃厚度 | - | 可使用或不使用盖板玻璃 |
| 0 | 不带玻璃盖使用 | |
| 0.17 | 规定的试样盖板玻璃厚度 | |
| 工作距离 | WD + number | 工作距离（毫米） |
| Phase, Ph, phaco, PC PH1, PH2, and so on | 使用各自相位聚光环的相位对比物镜 | |
| D | 暗场物镜 | |
| I, IRIS, W/IRIS | 内置光圈光阑，可调节 NA | |
| UV, UV-A | 透紫外线，波长低至 340 纳米 | |
| Ultrafluar | 荧光物镜，可在紫外和可见光区域进行低至 250 纳米的成像 | |
| DIC | 微分干涉相衬 | |
| L | 长工作距离 | |
| LL, LD, LWD | 超长工作距离 | |
表2.2 放大倍数的颜色编码
| Color code | Magnification |
|---|---|
| White | 100-160× |
| Dark blue | 60-60× |
| Light blue | 40-50× |
| Green | 16-32× |
| Yellow | 10× |
| Orange | 6.3× |
| Red | 4-5× |
| Brown | 2.5× |
| Gray | 1.6× |
| Blak | 1-1.25× |
表2.3 浸润介质的颜色编码
| Color code | Immersion |
|---|---|
| White | Water |
| Orange | Glycerol |
| Red | Multi-immersion |
| Blak | Oil |
5.4 浸润介质
物镜是显微镜的核心部件，其性能与使用方式密切相关。物镜可以分为两大类：干式物镜 (Dry Objectives)，在空气中使用；以及浸润式物镜 (Immersion Objectives)，需要与特殊的浸润介质配合使用。
5.4.1 干式物镜
干式物镜，也被称为“干镜片”，通常用于低倍率观察，可在有或无盖玻片的情况下使用。它们普遍使用的数值孔径（NA）上限约为0.25。对于NA值低于0.4的物镜，盖玻片厚度偏离标准值（通常为0.17毫米）的影响并不显著。然而，高倍率干式物镜的NA最大可达0.95，对应的孔径角接近72°。由于高NA会带来极短的工作距离（Working Distance, WD），最短可至100微米，这类物镜在操作上更为困难和关键。
5.4.2 浸润式物镜
许多物镜被设计用于在物镜前透镜和盖玻片之间填充折射率高于空气的介质，以提高成像质量。常用的浸润介质包括浸油、甘油或水。使用这些介质的主要目的是增加物镜的数值孔径（NA），从而显著提升图像的亮度和分辨率。
为了获得最佳的成像效果，理想的“均匀浸润”状态是让样本安装介质、盖玻片、浸润液以及物镜前光学元件的折射率尽可能匹配。这样做有助于在光线穿过这些界面时，避免产生球差 (Spherical Aberration) 和色差 (Chromatic Aberration)。由于这些介质可以被视为物镜前透镜的延伸，光线在其中的折射路径更为平直，同时也减少了界面上的反射，从而提高了图像对比度。
5.4.2.1 油浸物镜
油浸物镜是浸润式物镜中最常见的一类。为了充分利用其性能，通常需要使用折射率与玻璃相近的浸油、玻璃盖玻片，并尽量使用折射率与油相匹配的树脂来安装样本。
然而，使用高NA油浸物镜进行成像是一个对经验要求很高的过程，需要特别注意以下几点：
盖玻片厚度：高NA物镜通常针对标准的0.17毫米盖玻片厚度进行了优化，即使是同一批次的产品，厚度也可能存在差异（通常在120到200微米之间）。对于NA大于1.3的物镜，实际厚度与物镜上标示值的偏差不应超过±5微米，否则会引入显著的像差。
工作温度：浸润式物镜的设计温度通常为23℃。温度的偏离会导致物镜内部透镜因热胀冷缩而产生微小的移动，进而影响图像质量。为了将物镜和样本的升温降至最低，应尽可能降低照明光的强度，例如使用中性密度滤光片或减小灯电流。在没有校正环的情况下，也可以使用特定的浸油来补偿温度影响。
校正环：有些物镜配备了机械校正环，可以调整系统内透镜的位置，以校正不同温度或盖玻片厚度所引起的像差。
5.4.2.2 水浸物镜
对于水溶液中的样本，特别是活细胞观察，使用水浸物镜是一个很好的选择。这类物镜专门设计用于在水介质中直接观察活体生物样本。
在倒置显微镜上观察活细胞样本是一种非常普遍的应用，这通常需要在显微镜载物台上使用盖玻片，并将样本和浸泡液分开。在这种情况下，物镜前透镜与样本之间存在一个不均匀的光学系统。因此，强烈建议使用专用的水浸物镜，因为它们通过固有的光学设计来校正盖玻片-水界面上不可避免的显著球差，从而在样本深处也能提供非常好的图像。使用水浸物镜时，应使用蒸馏水或去矿物质水，以免因水干涸后留下沉淀物而难以清洁。
如果没有专用的水浸物镜，通常会使用油浸物镜作为替代。对于非常靠近盖玻片/缓冲液界面的薄样本，这种替代方法的效果出奇地好。然而，如果使用油浸物镜聚焦更深处的水溶液样本，图像质量会迅速下降。图2.22展示了点扩散函数（PSF）在这种情况下衰减的情况。
5.5 特殊应用物镜
工作距离 (Working Distance, WD) 是衡量物镜实用性的一个重要参数，它指的是物镜的前端与对焦样本（通常是盖玻片的最近表面）之间的距离。如果不使用盖玻片，工作距离则直接指物镜前端到样本本身的距离。在保持浸润条件的情况下，工作距离也等同于可以在样本内部清晰成像的深度。
对于高分辨率物镜，工作距离通常非常短，这是因为其数值孔径（NA）和孔径角必须尽可能大。例如，一个放大倍率为100倍、NA值为1.4的高倍物镜，其工作距离可能短于200微米；而一个NA值为0.2的10倍物镜，工作距离则可长达6毫米。为了保护物镜前透镜和样本，高倍率物镜的前端部分通常采用弹簧安装设计，以便在不慎与样本台接触时能够向物镜筒内滑动，从而避免损坏。
在某些特殊应用中，例如需要通过显微注射对活细胞进行操作时，则需要使用长工作距离（Long Distance, LD）物镜。尽管这类物镜在实现高数值孔径和良好像差校正方面存在挑战，但仍有专为此目的而开发的物镜。由于其复杂的光学结构，这类物镜通常价格相对较高，并且通常带有可调整内部透镜的机械校正环。
图 2.22：使用油浸物镜在水中成像时，盖玻片处产生的球差。
除了实现单纯的放大功能，物镜还需根据特定的成像技术而具备特殊的光学特性。
荧光显微镜物镜：对于荧光显微镜而言，物镜必须具备低本征自发荧光（autofluorescence）、低本征反射率以及在近紫外（Near-UV）波段具有高透光率等特性。这些特性主要取决于物镜所使用的玻璃类型以及镜片表面的特殊镀膜工艺。当今的物镜通常在360纳米以上的波长范围内，透射率可达到90%以上。如果物镜需要在此波长以下（即紫外光）工作并保持高透光率，则通常会有专门的标签进行标识。
对比技术物镜：专为特定对比技术（如相衬或DIC）设计的物镜，通常需要高度改进的光学特性，这些将在后续章节中进行详细讨论。
6 对比度
光拥有多种基本特性——包括相位、偏振、波长（或颜色）以及强度（或亮度）。光路中的物体通常会改变其中的一个或多个属性。然而，人眼和电子光探测器仅能直接感知光的波长和强度。因此，我们只能直接探测到改变这两种属性的物体。
这种能够改变穿过自身光波振幅的物体，被称为振幅物体 (Amplitude Object)。如果振幅的变化与波长相关，物体就会呈现出颜色。与此不同，只改变光波相位（可能以与偏振相关的方式）的物体，则被称为相位物体 (Phase Object)。这类物体的典型例子是透明的玻璃或晶体。由于与周围介质的折射率不同，这些物体会使穿过的光波产生相位延迟。此外，许多生物样本（如薄层细胞或组织）也会影响相位，但对光波的振幅影响很小。
即便一个相位物体被清晰放大，它也未必是可见的。要使物体可见，其颜色或光强必须与周围环境有足够的差异，换句话说，物体与背景之间的对比度 (Contrast) 必须能够被探测到。对比度指的是物体与背景在强度或波长上的差异程度。对于人眼而言，在明亮光线下感知所需的强度对比度可能低至0.02，但在光线不足时，则需要0.05。对于非常微小的物体，所需的对比度甚至需要达到0.2。物-景对比度的差异对于观察精细细节至关重要，因此为了清晰感知物体，对比度应尽可能高。
在显微镜的发展史上，为了使相位物体变得可见，人们开发了多种被称为光学对比方法 (Optical Contrast Methods) 的技术。这些技术在生物样本的显微观察中发挥着至关重要的作用。从原理上讲，对比技术可分为两大类：
化学方法：主要通过使用染料对物体结构进行选择性标记，从而引入颜色对比。在现代显微技术中，这主要指利用荧光染料进行标记，相关内容将在第3章和第4章深入讨论。
物理方法：旨在将最初难以察觉的相位差异转化为可感知的振幅或强度差异。目前，生物医学应用中最重要的物理光学对比技术是相位对比 (Phase Contrast) 和暗场对比 (Dark Field)。暗场对比是物理对比技术的一种便捷实现方式。
6.1 暗场显微术
暗场显微术是最简单的物理对比技术之一，也常被称为暗场照明。其核心原理是只让被样本衍射 (Diffraction) 或散射 (Scattering) 的光进入物镜，而将所有直射光阻挡在外。这可以通过从侧面照射样本来轻松实现。在透射光暗场模式中，可以从下方照亮样本，通过将入射光线的倾斜角度设置得很高，使其超过物镜的最大孔径角，从而确保物镜无法捕捉到任何直射光。
图 2.23 暗视野对比。(a) 暗视野照明原理；(b) 暗视野聚光镜。
如图2.23所示，当物镜的入射角度大于物镜的最大孔径角时，只有来自样本的散射光能够进入物镜，从而形成高对比度的图像。在这种设置下，物体背景完全变暗，只有那些能散射光的物体结构才显得明亮。
对于使用NA ≤ 0.4的低倍物镜，只需在聚光镜的前焦平面插入一个适当大小的环形光阑 (Annular Stop)，即可轻松实现暗场照明。为此，甚至可以使用相位对比聚光镜，因为其前焦平面也包含一个环形孔。该环形光阑能够阻挡照明光的中心部分。其优点是光阑位于聚光镜的正确前焦平面，并且可以通过调节螺钉进行中心定位。然而，缺点是聚光镜透镜表面的反射会减弱暗场效果。
当需要使用较高NA值的物镜时，则必须使用反射型专用暗场聚光器（如图2.23b所示）。与环形聚光器相比，这类反射型聚光器能产生更高的辐照度，并能使不同颜色的光产生相同的倾斜角度，从而形成更清晰的暗场照明锥。在物镜光轴上准确定位这些暗场聚光器非常重要。使用心形聚光器时，应在载玻片和聚光器表面之间添加浸泡液，以避免因物镜载玻片发生折射而降低有效倾角。
使用高NA值（例如NA 1.4）的聚光器尤为有利，因为在使用空气物镜观察时，照明光会在盖玻片的上表面完全反射，在这种情况下，照明光的消除特别彻底。一些物镜通过内部的孔径光阑可以调节NA值，这在实际操作中非常实用，因为可以通过调节NA，直到背景完全变暗。
原则上，也可以通过阻挡物镜后焦平面的照明光来获得暗场效果。不过，这种方法会损失相当数量的衍射光，因此需要使用为暗场观测专门设计的物镜。
7 相位对比显微术
相位对比（Phase Contrast）显微术与后续将要描述的干涉对比方法，其核心原理都是将穿过样本后发生衍射的光与未被样本改变的背景光（或称未衍射光） 在空间上分离开来。通过对这两束光分量的振幅和相位进行精确操控，使它们在最终成像时发生相长或相消干涉，从而将人眼无法直接感知的相位差异，转化为可被观察到的振幅（亮度）差异。
这项极具实用价值的技术由物理学家弗里茨·泽尔尼克（Frits Zernike）于1932年提出，旨在解决在普通明场显微镜下几乎不可见的相位物体的观察难题。他通过一系列构思精巧的实验，不仅优雅地阐明了其对比技术的原理，也生动地诠释了显微镜成像的波动光学理论。由于他的实验极具启发性，我们将在此详细介绍其论证过程。
7.1 泽尔尼克的思想实验
泽尔尼克通过一系列逻辑递进的实验，揭示了相位对比的奥秘。
实验1：观察振幅物体
设置：在标准明场显微镜下观察一个微小的振幅物体（例如一个小墨点）。
观察：在明亮的背景上看到一个暗点。
物理解释：这是因为物体衍射出的光波，相对于未衍射的背景光，产生了180°的相位偏移。这导致两束光在像平面上发生相消干涉，从而形成了暗像。
实验2：分离衍射光与背景光
设置：将聚光镜光圈缩小为一个点光源，并在与聚光镜光圈共轭的物镜后焦平面上，放置一个同样大小的遮光点，用以阻挡所有未衍射的背景光。
观察：此时，图像背景变暗，而物体本身则呈现为一个亮点。
物理解释：图像完全由衍射光形成。由于没有背景光参与，无法发生干涉，我们看到的是衍射光自身的亮度。
图2.24 泽尼克第二个实验。(a) 显微镜的照明光路；(b) 成像光路。箭头指示下方草图中的相应平面。(c) 放大图显示聚光镜前焦面与物镜后焦面之间的空间。未衍射光和衍射光分别以蓝色和红色显示。浅蓝色标记的四个平面将在图2.25中进一步讨论。
图2.25 泽尼克实验中的掩模、物体、图像、相位和振幅。 第一列和第三列分别描述了聚光镜前焦平面和物镜后焦平面上的掩模。在上方的两个实验中，检查了吸收物体；在下方的三个实验中，检查了透明或相位物体，如第二列所示。第四列概述了最终图像，第五列用所谓的相量图表示了相关波的相对相位和振幅（蓝色，未衍射的背景光；红色，衍射的物体光；黑色，通过矢量相加其他两个分量得到的物体位置处的合成波）。
实验3：观察相位物体
设置：在标准明场显微镜下观察一个相位物体（例如一个透明的微小玻璃颗粒）。
观察：在明亮的背景下，几乎看不到任何物体。
泽尔尼克的假设：如果相位物体的衍射光也像振幅物体一样有180°的相移，那么它在明场下也应该是暗的。既然它不可见，泽尔尼克大胆假设：相位物体的衍射光相对于背景光，仅有约90°的相位偏移。当一个振幅很弱、相位偏移90°的衍射波与一个振幅很强的背景波叠加时，最终合成波的振幅变化极小，因此无法产生足够的对比度。
实验4：验证假设并创造对比度
设置：为了验证上述假设并解决问题，泽尔尼克设计了一种特殊的相位板 (Phase Plate)，并将其放置在物镜的后焦平面。这个相位板有两个关键功能：
减光：相位板中心有一个吸收层，可以将未衍射背景光的振幅（亮度）降低到与衍射光几乎相同的水平。
移相：相位板中心周围的区域可以将穿过的衍射光再额外延迟90°。
观察：经过这样处理后，原本透明的相位物体在灰色的背景上呈现为一个清晰的暗像。
物理解释：这一结果完美验证了泽尔尼克的假设。衍射光经历了物体本身带来的90°相移和相位板带来的额外90°相移，总相移达到了180°。此时，振幅相近、相位相反的衍射光与背景光在像平面上发生了剧烈的相消干涉，从而产生了极高的图像对比度。
结论：可观察到的图像对比度，取决于物体的物理特性、照明模式，以及对背景光和衍射光的选择性操控。这两种光在物镜的后焦平面上是空间分离的，因此可以被独立地进行处理。
7.2 相位对比显微镜的构造
在实际的相位对比显微镜中，实验中的点状光阑被替换为环形光阑 (Annular Stop)，放置于聚光镜的前焦平面。这使得更多的光能够到达样本，从而获得更明亮的图像，并增大了聚光镜的有效NA，提高了光学分辨率。
与此对应，物镜后焦平面的相位板也被制作成一个互补的相位环 (Phase Ring)。
相位环：这个环形区域带有吸收层（用于减弱背景光）并且具有不同的厚度，以实现所需的90°（λ/4）相移。
波长依赖性：相位环产生的相位延迟量与光的波长有关，通常被设计为对人眼最敏感的绿色光（约550纳米）产生精确的90°相移。因此，在进行高质量的相衬观察时，常在照明光路中插入绿色滤光片。
对中要求：为了达到最佳效果，来自聚光镜环形光阑的照明环成像，必须与物镜中的相位环精确重合。由于不同放大倍率和NA的物镜需要不同尺寸的相位环，因此通常会将多个环形光阑安装在一个可旋转的聚光镜转盘上，以便与不同的相衬物镜匹配。
校准：操作者需要使用一个特殊的对中望远镜（或称为辅助显微镜、贝特朗透镜）来代替目镜，直接观察物镜的后焦平面，并通过调节螺丝将照明环与相位环精确对齐。
由于相位环内置于物镜内部，因此用于相衬成像的物镜是特殊设计的产品。在普通明场模式下使用时，相位环会略微降低图像亮度。此外，相位对比物镜在落射照明技术（如荧光显微镜）中尤其不利。
7.3 相位对比图像的特性与局限
图像解读：相位对比图像并非物体形态的简单再现，其对比度源于对衍射光和背景光的特殊处理，因此图像的解读需要一定的经验。
适用范围：该技术最适用于相位延迟较小的薄样本，例如单层细胞或组织切片。理想的相移范围最高约为30°。如果物体造成的相位延迟过大（例如超过45°），对比度会下降，甚至发生衬度反转（暗的变亮，亮的变暗）。
光晕效应 (Halo Effect)：由于相位环的宽度有限，衍射光与背景光的分离并不完美。这导致在明暗边界处，暗物体的周围常常会出现一圈明亮的光晕，这可能会对物体边界的精确识别造成干扰。
对比度调节：如果样本本身的相移过小或过大，可以通过改变样本封片剂（或称安装介质）的折射率来调节相移量，从而优化对比度。因为相移量正比于物体的光程长度以及物体与周围介质的折射率之差。
8 干涉对比显微术
解决相位物体观察问题的核心方法，是将物体与其周围环境之间难以察觉的相位差转化为人眼或探测器可以感知的振幅差（即亮度差）。为此，我们需要设法改变衍射波的相位，使其与未衍射的背景波在像平面上发生相消干涉。泽尔尼克（Zernike）通过在物镜后焦平面上操控空间分离的波分量实现了这一目标。除此以外，还有其他技术可以有效地达到同样的目的，这些技术统称为干涉对比 (Interference Contrast)，并且在某些方面甚至比相位对比技术更为灵活。
基本原理
干涉对比技术的主要原理如图2.26所示：在到达样本之前，照明光被分光器分离成两束相干的波列。
样本光束 (Sample Beam)：其中一束穿过装有待测物体的样本区域。
参考光束 (Reference Beam)：第二束光，即参考波，沿着一条与样本光束光程长度相同的路径传播，但不经过物体。
图 2.26 干涉相衬原理。
此外，我们还可以在参考光束的路径中插入一个可移动的玻璃楔 (Glass Wedge)，通过改变其位置来精确地引入一个可控的相位延迟。当这两束光重新汇合时，它们会发生干涉，从而在像平面上形成具有对比度的图像。
灵活的对比度控制
这种装置使得操作者能够实现比相位对比更强大的功能，因为它可以自由地对衍射光和背景光的振幅与相位进行操控。最终的图像是由三种不同波列干涉产生的：来自物体的衍射波、穿过样本区域的未衍射光，以及未衍射的参考波。
图2.27 干涉相衬。 顶部的示意图展示了相关波之间的相位关系。样品室背景波的相量用蓝色表示，参考波的相量用红色表示。物体衍射波的相量用绿色箭头表示，总背景波的相量用黑色表示。(a) 波的相长干涉；(b) 因180°相位差导致的相消干涉；(c) 参考波中约∼225°的相移导致与样品室中的背景波相比，两个波的总和产生约∼270°的整体相移。请注意，样品室中的亮度也略有降低。(d) 在样品室中引入一个相位物体。它衍射出一个90°相移的物波。270°相移的背景将与物波发生相消干涉。
通过调节玻璃楔，我们可以任意改变参考波的相位，从而精确控制背景光的最终相位。这样，无论物体本身产生的实际相位偏移是多少，我们总能调整背景光的相位，使其与衍射光的最终总相位差达到180°（相消干涉的条件）。
背景调节：在没有样本的情况下，如果我们将玻璃楔完全移出光路，两束光的光程完全相同，它们会发生相长干涉，产生一个均匀、明亮的背景。如果我们将玻璃楔移入，使参考光束产生180°的相位延迟，那么两个未衍射波就会处处发生相消干涉，导致背景完全变暗。
产生对比度：我们可以将背景光的相位调节到一个特定值（例如270°）。当放入一个相位物体时，其衍射波会产生约90°的固有相位延迟。此时，90°相移的衍射波与270°相移的背景波之间恰好相差180°，两者发生相消干涉，从而在明亮的背景上形成一个清晰的暗色物像。
高级功能与局限性
强大的适应性：由于我们可以任意选择背景光与衍射光的相位关系，因此不仅可以实现从正衬度（暗物像）到负衬度（亮物像）的切换，还可以针对不同相移特性的物体进行优化，以获得最佳对比度。
定量测量：通过在背景波中引入已知的相移，我们甚至可以精确测量由物体产生的相位延迟，从而推算出其折射率或物理厚度的信息。
然而，这种多功能性是有代价的。干涉显微镜需要非常特殊且复杂的光学装置，包括用于分离、重组和精确调相的元件。实现样本光路和参考光路之间极其精确的长度匹配，在技术上也非常具有挑战性。
尽管如此，我们在此不会深入探讨这种通用干涉显微镜的光学设置，因为它引出了一种更为重要且应用广泛的相关技术，即当今在医学和生物样本观察中占据核心地位的微分干涉对比 (DIC)。
9 高级主题：微分干涉对比 (DIC) 显微术
微分干涉对比 (Differential Interference Contrast, DIC) 显微术是一种功能强大的技术，用于增强相位物体的对比度。DIC 可用于透射光或反射光，但在生物医学应用中，透射光DIC更为重要。要理解其工作原理，需要对光的干涉、相干、偏振以及偏振元件（如起偏器和检偏器）有深入的了解。
9.1 DIC显微镜的光学构造
DIC显微镜的光学装置巧妙地利用了聚光镜前焦面与物镜后焦面之间的光学共轭关系。其光路相对复杂（如图2.28所示），主要由以下关键元件构成：
起偏器 (Polarizer)：位于照明光源和聚光镜之间，产生特定方向（例如45°）的线偏振光。
第一块沃拉斯顿棱镜 (Wollaston Prism)：放置于聚光镜的前焦平面。它是一种特殊的光学元件，能将入射的偏振光分解为两束振动方向相互垂直（例如，水平和垂直偏振）且传播方向有微小夹角的相干光束。
剪切效应 (Shear)：由于棱镜位于聚光镜的前焦面，经过聚光镜后，这两束不同偏振的光会变成两束平行的光束照射到样本上，但它们之间存在一个微小的横向位移，这个位移被称为“剪切”。剪切的距离由棱镜的结构决定，并且其大小被设计为小于所用物镜的光学分辨率。
第二块沃拉斯顿棱镜：放置于物镜的后焦平面，负责将穿过样本的两束剪切光束重新合并。这块棱镜可以横向移动，通过改变两束光在棱镜内的光程，来精确地引入一个可调的额外相位延迟Δ。
检偏器 (Analyzer)：位于第二块棱镜之后，其偏振方向通常与起偏器正交。它只允许重新合并后的光束中特定偏振方向的分量通过，从而使两束光发生干涉。
对比度的产生机制
DIC图像的最终对比度，源于穿过样本相邻微小区域的两束剪切光之间的光程差 (Optical Path Difference, OPD)。
背景：在样本的平坦区域（背景），两束剪切光穿过的光程完全相同。当它们被第二块棱镜合并后，会恢复成原始的45°线偏振光。由于检偏器的方向与起偏器正交，这束光会被完全阻挡，因此背景是暗的（假设Δ=0）。
边缘检测：当这两束光扫过一个相位物体（如细胞核）的边缘时，其中一束光穿过了物体，而另一束光仍穿过背景。穿过物体的光束会因为折射率或厚度的差异而产生一个额外的相位延迟。这导致两束光在合并后，其偏振状态不再是线偏振，而是变成了椭圆偏振。
从偏振到强度：椭圆偏振光中含有能够通过检偏器的分量，因此在图像的这个位置，检偏器不再能完全阻挡光线，从而产生了亮度。简而言之，DIC系统将样本微小区域的相位梯度（光程差的变化）巧妙地转化为了可见的亮度差。
伪三维效果与Nomarski DIC
由于对比度只在发生光程差变化的方向上产生，因此DIC图像具有很强的方向性。通过移动第二块棱镜来调整相位延迟Δ，可以使物体的一个边缘变亮，而另一个边缘变暗。这使得图像呈现出一种独特的、类似浮雕的伪三维效果，仿佛物体被从一侧照亮并在另一侧投下阴影。
传统的DIC需要将厚重的沃拉斯顿棱镜精确地置于物镜内部的后焦平面，这使得物镜成为专用且不便更换的部件。为了解决这个问题，法国物理学家乔治·诺马斯基（Georges Nomarski）发明了一种改良的棱镜，即诺马斯基棱镜 (Nomarski Prism)。这种棱镜可以将光束的重组平面置于棱镜之外，因此可以方便地安装在物镜上方，并且可以轻松拆卸。这种改良技术被称为诺马斯基DIC，由于其便利性和卓越的性能，已成为当今生物科学领域应用最广泛的干涉对比技术。
9.2 DIC图像的解读
伪三维浮雕：DIC图像标志性的三维浮雕感是一种光学伪影 (Artifact)。它反映的是样本光程差的梯度，而非真实的物理拓扑结构。图像中的“山峰”和“峡谷”可能仅仅是由折射率的微小变化引起的，而物体的实际厚度可能完全是平坦的。
方向性：DIC图像不具备旋转对称性，它只显示沿剪切方向的光程差梯度。为了全面了解物体的结构，使用可旋转的载物台进行观察会很有帮助。
出色的光学切片能力：DIC对样本的轴向（深度）位置变化极为敏感。焦平面以外的物体特征不会干扰成像，因此它可以获得非常薄的光学切片，非常适合观察厚样本。
9.3 DIC与相位对比的比较
尽管DIC和相位对比的应用场景有所重叠，但它们之间存在显著差异：
| 特性 | DIC (微分干涉对比) | 相位对比 (Phase Contrast) |
|---|---|---|
| 成像原理 | 显示光程差的梯度，具有方向性 | 显示物体的光程差本身，旋转对称成像 |
| 图像外观 | 伪三维浮雕效果 | 物体周围有**光晕 (Halo)**伪影 |
| 分辨率 | 较高，无光晕干扰 | 略低，受光晕影响 |
| 光学切片 | 非常出色，适合厚样本 | 较差，景深大，不适合厚样本 |
| 适用样本 | 薄样本和厚样本均有良好对比度 | 最适合相位延迟小的薄样本 |
总而言之，与相位对比相比，DIC技术要求更高、设备更复杂，但其应用范围更广，尤其在需要高分辨率和光学切片能力的厚样本观察中，具有不可替代的优势。
10 本章总结
本章全面概述了光学显微镜的基本原理。现代显微镜的核心成像元件是物镜与管镜，它们通常构成一个无穷远校正装置。整个显微镜系统包含照明与成像两个互补的光路，每个光路都由特定的组件和共轭光学平面组成。其中，柯勒照明作为标准的照明方式，不仅能提供均匀的照明，还能将照明视场与孔径分离开来，并在聚光镜和物镜的前焦平面上形成共轭光学平面，为高级对比技术奠定了基础。
从波动光学的角度来看，图像的形成是一个基于衍射和干涉的复杂过程。物镜的后焦平面包含了物体的衍射图样，它对应于物体函数的截断傅立叶变换。最终的图像是物体与系统点扩散函数（PSF）的卷积，这意味着透镜系统在本质上是一个低通滤波器，会过滤掉物体最精细的结构信息。因此，光学分辨率存在一个物理极限，该极限由瑞利判据（0.61λ/NA）给出，并且相干与非相干物体的分辨率限制有所不同。为了充分利用这一分辨率，必须选择与探测器尺寸相匹配的最佳放大倍率。
物镜作为显微镜的心脏，其特性直接决定了成像质量。理想的物镜应是远心的，以保证放大倍率的稳定性。物镜的类型和像差校正水平各不相同，但总会存在一定的残余像差。图像亮度通常与物镜数值孔径（NA）的平方成正比，与放大倍率的平方成反比；而在荧光显微镜中，亮度则随NA的四次方急剧增加。因此，为特定应用仔细选择合适的物镜是获得满意成像效果的关键。
最后，对于生物医学应用中常见的透明样本，必须使用特殊的光学对比技术才能使其可见。其中，相衬（Phase Contrast）和微分干涉对比（DIC）是最重要的两种技术。这些技术的基本原理都是通过对背景光和物体衍射光进行选择性操控，从而将不可见的相位差异转化为可被探测的强度差异。