荧光显微成像系列——共聚焦显微镜

传统宽场显微镜的发展与局限

传统的宽场荧光显微镜（参见第1章和第2章）以其相对较低的技术难度揭示了微观世界的细节，令观察者着迷。科学家们一直在不懈努力，寻求增强这一强大工具的方法，并取得了显著进展。在光学显微镜的悠久历史中，罗伯特·胡克是早期的开拓者之一。他于1665年出版了开创性的著作《显微术》，被认为是光学显微镜发展的奠基人之一。然而，胡克显微镜的能力在当时受到镜片质量的限制，质量相对较差。与胡克同时代的安东尼·范·列文虎克是一位卓越的镜片研磨师，他能够制造出出色的短焦距镜片，大大提高了显微镜的分辨能力。范·列文虎克制造的显微镜使用的是单透镜，因此从技术上讲，它们只是简单的放大镜，但却能放大200-300倍，从而首次对微观世界进行了细致的观察。范·列文虎克的研究成果至今仍被认为是独一无二的，从他的描述和绘图中，我们很容易辨认出他观察到的细菌（被称为动物）或藻类。显微镜的下一个重大突破发生在200年后的1846年，卡尔·蔡司开始制造空间分辨率不再受技术限制的光学显微镜。他与恩斯特·阿贝（Ernst Abbe）合作，提出了光学显微镜分辨能力的理论推导。他对乔治·艾里（George Airy）早先提出的理论进行了扩展，指出显微镜物镜有限开口上的光衍射是限制分辨率的最主要因素。通过具有圆形孔径的理想透镜聚焦的光的衍射图样可以用艾里斑来描述。其大小取决于角孔径α和周围介质的折射率n。在这种情况下，他还创造了数值孔径（NA）一词，定义为NA = n sin α（参见第2.2.4节）。阿贝与赫尔曼·冯·亥姆霍兹（Hermann von Helmholtz）一起描述了物体被分开后仍能分辨的最小距离Δx：

其中𝜆是光的波长。后来，瑞利爵士考虑到理想的点状物体如何在三维空间中成像。根据瑞利判据，两点刚好可以分辨的距离Δx相当于从艾里斑中心到其第一个最小值的距离（图2.9b）:

关于瑞利判据的正式和更详细的描述见第2章。尽管瑞利判据经常被用于估算显微镜的衍射极限分辨率，但显微镜的实际分辨能力取决于图像对比度和光子统计，或者更一般地说，取决于测量的信噪比。这促使天体物理学家斯帕罗（C.M. Sparrow）提出了另一种分辨率极限规范（斯帕罗判据）。如图2.10c所示，在两个点扩散函数（PSF）之间的凹陷不再能被检测到之前，两个信号仍然是可分辨的。造成宽场显微镜对比度过低，从而限制其分辨能力的原因有几个。首先，假设样品的吸收可以忽略不计，宽场显微镜中的激发并不局限于焦平面。探测器上产生的图像也不局限于来自焦平面的信号。然而，不在探测器和物镜焦平面上的点会在焦外成像，其强度会在空间中分散，从而增加背景信号。此外，特别是在生物样本中，散射效应（如廷德尔效应）非常常见。这种效应描述的是大小与光波长相当的颗粒对光的散射。由于光的散射，原本来自样品焦外区域的光子可能会重新定向到焦平面，随后形成漫反射背景。限制空间分辨率的往往是低图像对比度，而不是纯粹的波动光学标准。因此，显然必须找到提高图像对比度的新方法，以拓宽光学显微镜的现有应用领域。

共聚焦显微镜理论

共聚焦显微镜原理

20世纪50年代末，马文·明斯基（Marvin Minsky）发明了共聚焦显微镜，其目的是能够在脑组织等致密组织中进行成像。共聚焦显微镜的关键在于使用两个针孔来限制激发光束和检测光束，从而抑制来自焦平面外的光信号。这两个针孔都位于显微镜的像平面上，因此是“共”焦的。

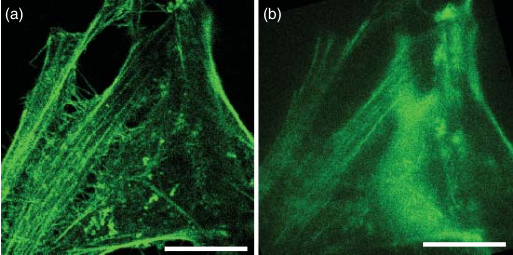图 5.1 HeLa 细胞肌动蛋白丝的共焦和宽场图像。(a) 在扫描共聚焦显微镜上，肌动蛋白丝清晰可见，没有焦外荧光造成的模糊。(b）相应的传统宽场显微镜图像模糊不清，可见高荧光背景。

图5.1展示了共聚焦显微镜的切片功能。我们使用Alexa Fluor 647标记的鬼笔环肽对HeLa细胞中的肌动蛋白丝进行染色。共聚焦荧光图像能够清晰地展示复杂结构的三维细节（见图5.1a），而宽场显微镜则无法呈现这些细节（见图5.1b）。现代共聚焦显微镜的光路示意图如图5.2a所示。为了便于比较，我们在图5.2b中也提供了自制共聚焦显微镜的示意图。

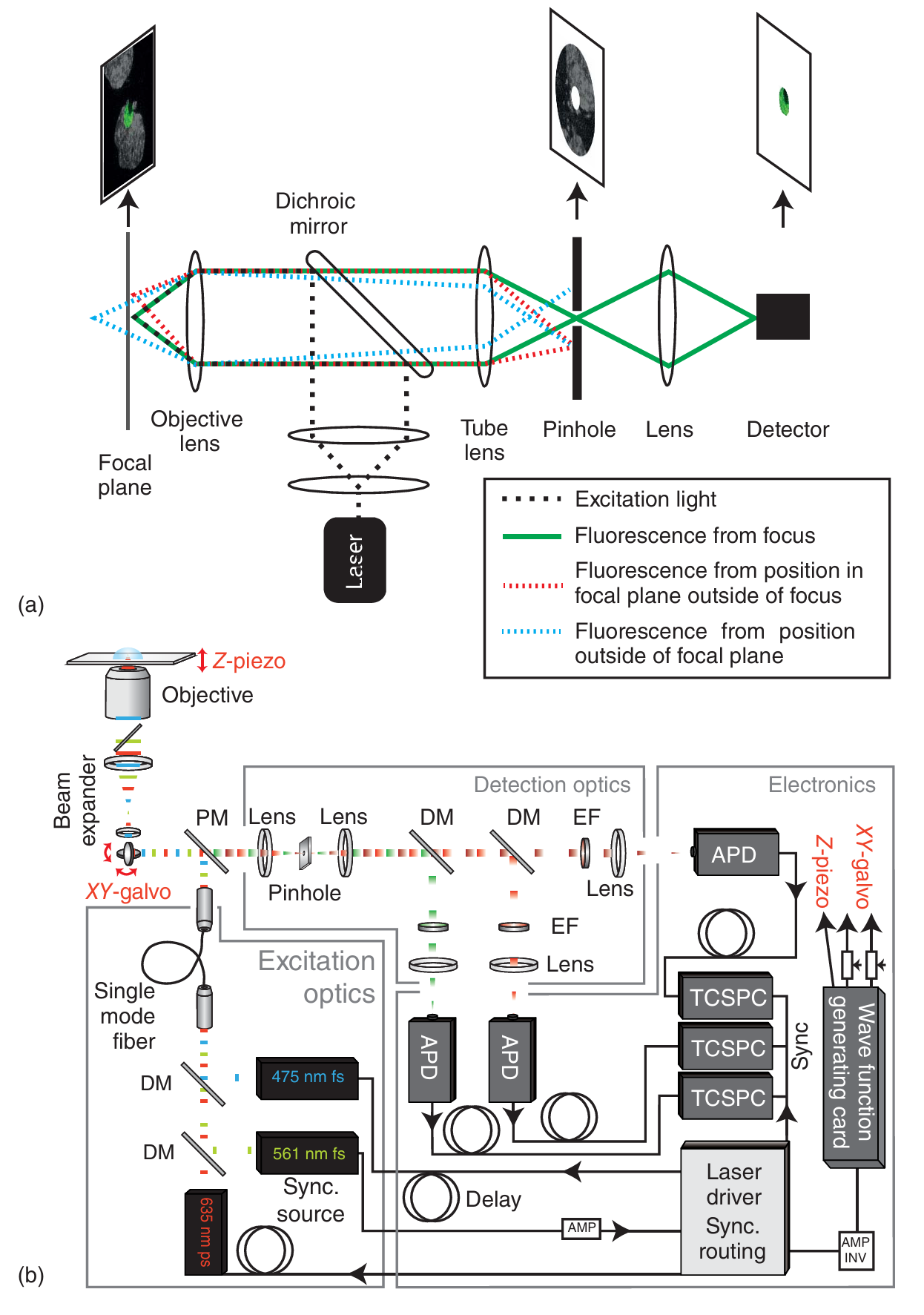图 5.2 共聚焦显微镜原理。(a) 简单的共聚焦显微镜示意图，激发光束（虚线，黑色）聚焦到样品上，来自焦点的光将穿过针孔到达检测器（实线，绿色），而来自邻近焦点位置（虚线，红色）或不同焦平面的光（虚线，蓝色）将被针孔截断。(b) 先进激光扫描共聚焦显微镜的实验实现示例。在这种情况下，选用脉冲激光作为激发光源，而不是共聚焦显微镜通常使用的连续波激光。激光器通过二向色镜 (DM) 组合在一起。在这种设置中，其中一个激光器还充当主时钟，使整个系统同步。激发光通过单模光纤射向显微镜物镜，XY 振镜系统用于激光扫描。荧光由同一物镜收集，由振镜去扫描，并由多面镜（PM）与激发光分离。荧光通过共焦针孔后，使用 DM 按颜色进行分离。随后使用适当的发射滤光片（EF）对光谱进行净化。雪崩光电二极管（APD）被选为收集荧光光子的探测器。光子计数随后通过时间相关单光子计数（TCSPC）电子装置进行登记。

通常情况下，相干激光束被选作激发光源（如图5.2a中黑色虚线所示），在这种情况下，激发针孔则不再必要。激发光束首先经过一组透镜进行扩展，随后通过分色镜反射。分色镜能够根据激发光和荧光信号（如图中绿色实线所示）的不同波长将它们分离。荧光信号由同一物镜收集，并通过分色镜传输至后续光路。为了确保只有来自样品某一特定区域的光线能够到达检测器，样品的成像平面上设置了一个针孔。共聚焦检测针孔决定了哪些光线能够到达检测器：来自激发光束焦点的荧光光子能够穿过针孔并被检测到（如图5.2a中的绿线所示）。而焦外光线（即与针孔不共焦的光线，如图5.2a中的蓝线所示）则会被针孔阻挡。例如，图5.2a中的蓝线描绘了来自样品不同轴向平面的光子路径。这些光线在显微镜内部的不同位置聚焦，相对于针孔平面而言是失焦的，因此大多数光线都会被针孔挡住。同样，来自焦平面但与样品平面针孔位置横向偏移的背景光（如图5.2a中的红线所示）也会被针孔阻挡。

尽管到达检测器的光线数量减少，但与明场成像方法相比，共聚焦针孔能够显著提高图像的信噪比。由于只有来自焦平面的光子能够被检测到，因此可以实现对样品的光学切片，如图5.2a中光路图上方展示的细胞共聚焦图像示例所示。在下一节的数学讨论中，将看到，在正常情况下，针孔的主要作用是产生Z轴分辨率，而对横向分辨率的影响相对较小。经过针孔后，剩余的光束可以直接照射到检测器上。检测器可以是光电倍增管（PMT）、雪崩光电二极管（APD），或者在某些情况下，也可以是电荷耦合器件（CCD）相机，例如在旋转盘共聚焦显微镜（SDCM）中。

在针孔之后的光束路径设计中，可以融入更多种类的光学元件。例如，如图5.2a所示，可以通过采用单透镜，在探测器表面为针孔形成清晰的像，或者添加偏振分光镜、二向色镜等其他光学器件以拓展功能。在此情形下，建议在安装这些附加光学元件之前，先对穿过针孔的光线进行重新校准，以确保光束能够准确地聚焦到相应的检测器上。

共聚焦显微镜成像的另一个核心要素是扫描技术。由于共聚焦显微镜的检测范围通常受到衍射极限的限制，因此它无法像宽场显微镜那样一次性记录整个图像。为了获取完整的空间信息，可以通过移动样品（相对于固定的光路系统）或在样品表面扫描激光束来实现逐点成像。有关共聚焦激光扫描方法的更多详细信息，请参阅第5.2.3节。

在共聚焦显微镜系统中，针孔扮演着至关重要的角色，它对于提高仪器的分辨率和切片能力起着关键作用。为了更全面地理解这一技术，有必要对图像形成的过程以及针孔在其中所起的作用进行简要探讨。当使用理想透镜（即仅考虑衍射效应，忽略透镜可能产生的色差或球差）对点状物体进行成像时，其强度分布遵循艾里斑（Airy pattern）的规律。从数学的角度来看，艾里斑是光圈函数傅里叶变换的平方模的表现形式。

其中，J₁ 是一阶贝塞尔函数的第一种。一个系统的分辨率被定义为两个点状物体仍能分辨的最小距离。利用瑞利准则，理想镜头的最小横向分辨率 r_lateral 为

在公式中，系数 1.22 来自艾里斑模式中贝塞尔函数的第一个零点。λ₀ 是光在真空中的波长，而 NA_Objective 和 NA_Condenser 分别代表物镜和聚光镜的数值孔径。通常情况下，物镜的数值孔径（NA）和聚光镜的数值孔径是相互匹配的，或者在实验中使用外荧光进行测量（即通过同一物镜完成照明和检测）。在这种情况下，公式（5.4）可以简化为

其中，r_lateral 是艾里模式中最大值到第一个最小值的距离。将公式（5.5）的结果乘以仪器的总放大倍率，即可计算出针孔平面内的艾里斑半径。其直径 d（即 2r_lateral）被称为 1 艾里单位（AU）。艾里单位与艾里模式的半最大全宽（FWHM）之间的关系为

需要注意的是，公式（5.4）及其推导是基于准轴近似，即假定在 x-y 平面传播的电磁场分量比在 z 方向传播的电磁场分量小得多。幸运的是，Novotny 和 Hecht 的研究表明，即使对于高数值孔径（NA）的物镜，准轴近似仍能获得相当准确的结果。否则，就需要对电磁场进行全面的矢量描述，以处理高数值孔径光学系统中的复杂情况。

图 5.4 PSF 与高斯近似示意图

到目前为止，仅探讨了镜头孔径衍射对图像形成所产生的影响。在共聚焦显微镜的工作过程中，激发光首先经由物镜聚焦至样品表面，随后，由同一个物镜负责收集样品所发出的荧光，并通过针孔将其导向检测器。为了精确计算出共聚焦显微镜的光学分辨率，必须综合考虑衍射对激发光束路径以及发射光束路径所带来的双重影响。依据第2章中所阐述的点扩散函数（PSF）理论，当针孔尺寸较小（d ≤ 0.5 AU）时，共聚焦显微镜的总PSF可以近似地看作是激发PSF与检测PSF两者的乘积。

对于较大的针孔，检测PSF的艾里模式必须与针孔的传递函数进行卷积。这意味着总共聚焦PSF可以视为检测PSF与激发PSF的乘积，再与针孔的传递函数进行积分。从数学角度来看，这等同于先将激发PSF和检测PSF进行卷积，然后将卷积结果与针孔的传递函数相乘。图5.4展示了针孔在一维情况下的影响。

艾里模式的径向依赖性可以用高斯函数很好地近似。一维高斯函数的强度分布I(r)的表达式为：

其中，r₀ 为高斯峰的中心位置，σ 为标准偏差，I₀ 为振幅。在外荧光测量中，激发和检测的点扩散函数（PSF）大小相等，即激发PSF和检测PSF的强度分布相同（I_Exc(r) = I_Det(r) = I(r)）。因此，总PSF可以表示为两个高斯函数的乘积，而乘积结果本身也是一个高斯函数：

由此产生的高斯的标准偏差（以及 FWHM）降低了 倍，从而使共聚焦显微镜的横向分辨率提高了 倍：

假设激发和检测 PSF 相等，全三维共焦 PSF 如图 5.5 所示。 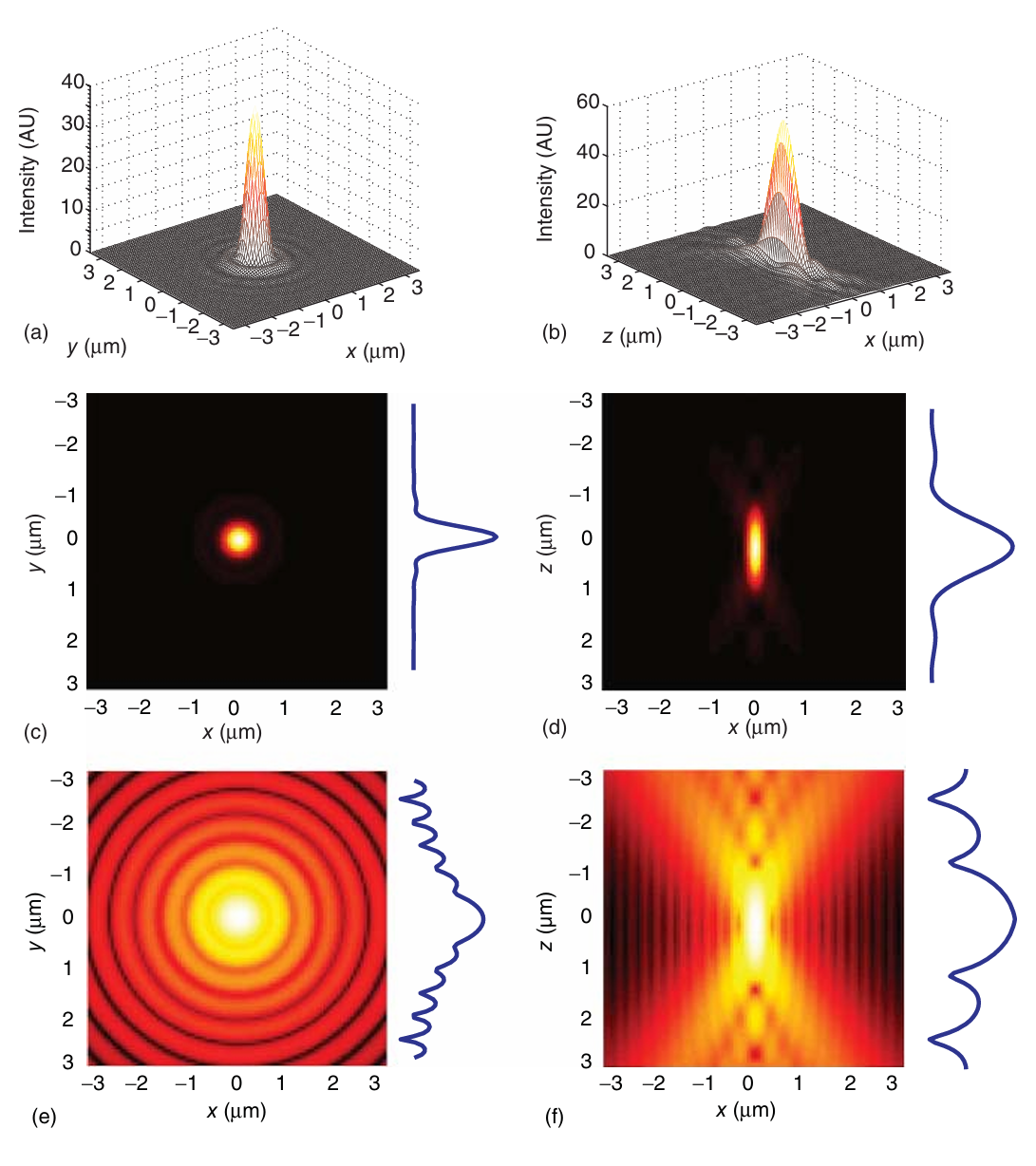图 5.5 发光点光源产生的空气图案。(a、b）PSF（a）横向和（b）轴向的三维表示。(c-f）整个焦点的强度分别在 x-y 平面和 x-z 平面上的投影，（c、d）为线性比例，（e、f）为对数比例。图像右侧的图中显示了通过所显示 PSF 中间的横截面。

针孔的大小可以调整，以改变分辨率或增加光通量。图5.6中绘制了轴向和横向全宽以及从显微镜焦点上的点光源检测到的光的分数与针孔大小的函数关系图。使用Novotny和Hecht 的公式（4.44）计算了数值孔径（NA）为0.5、放大倍数为60倍、激发波长为500 nm的物镜的激发和检测PSF。当针孔直径约为1艾里单位（AU）时，检测率到达一个高点。当针孔大小等于艾里模式的最小值时，就会出现高原。由于在PSF的最小值处没有强度，因此针孔大小的微小变化不会导致测量强度的变化。在针孔大小为1 AU的情况下，从点状光源收集到的光有86%通过针孔。由检测PSF确定的横向分辨率接近宽场检测所达到的分辨率，但针孔仍会影响轴向分辨率。

对于共聚焦显微镜的大多数应用而言，针孔尺寸在0.8至1.0 AU之间最为理想。选择明显小于1 AU的针孔尺寸（通常直径小于0.25 AU）可提高横向和轴向分辨率。在这种情况下，与公式（5.6）相比，横向分辨率可提高1.4倍：

然而，分辨率的提高是以光强度显著降低为代价的。当针孔大小为0.25 AU时，仅有约20%的收集光子能够通过针孔。如果将针孔尺寸增大到1 AU以上，横向分辨率并不会发生显著变化，因为此时分辨率主要受到激发PSF的限制。相反，光学切片厚度对针孔大小非常敏感，这在测量实际物体时显得尤为重要。相比之下，宽场显微镜的光学切片厚度并非由光学元件决定，而是由样品本身的厚度所决定。如果样品本身足够薄，宽场显微镜可以生成生物物体的锐利图像；否则，焦平面的锐利图像可能会因焦外光的干扰而变得模糊。

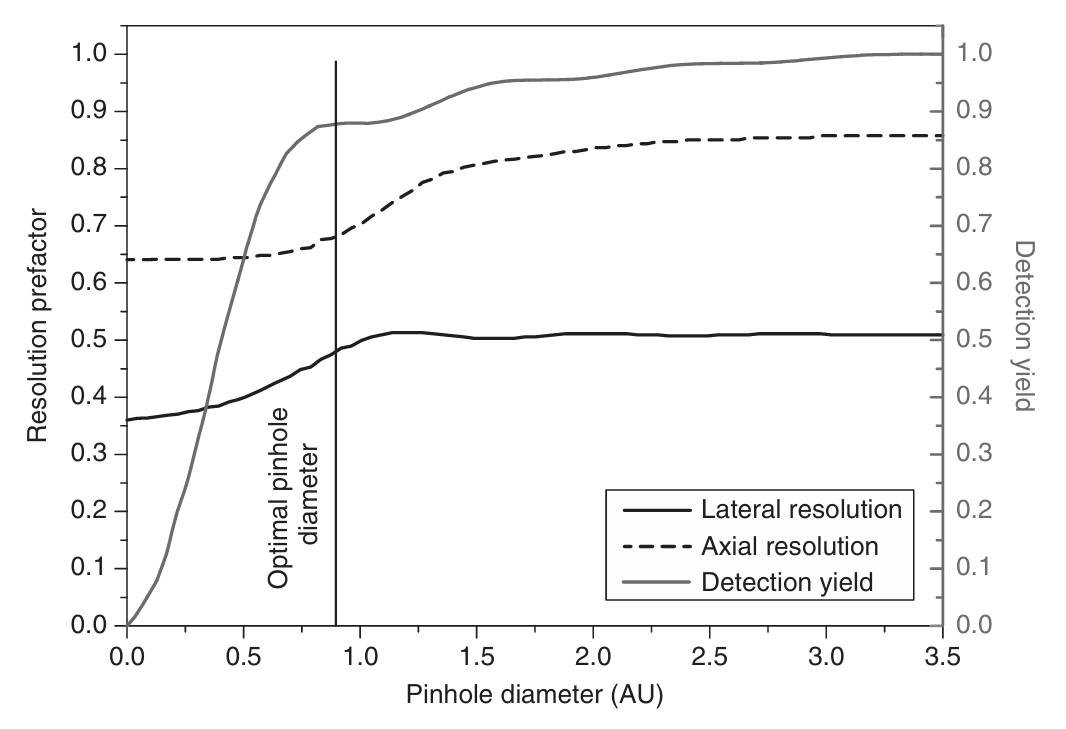图 5.6 展示了分辨率和信号吞吐量随针孔尺寸变化的关系。图中黑色实线和虚线分别表示横向和轴向分辨率的前因子变化（以 λ₀/NA_Objective 为单位，左侧刻度）。这反映了横向分辨率从公式（5.5）到公式（5.11）的过渡，以及轴向分辨率从公式（5.13）到公式（5.15）的类似变化。灰色曲线则表示检测率随针孔直径的变化（右侧刻度）。

在共聚焦显微镜中，光学厚度由针孔大小以及激发和检测 PSF 的乘积决定。检测 PSF 的深度由发射光的衍射图样和针孔的几何光学影响决定。探测 PSF 的轴向 FWHM 取值为

其中，PH 是针孔在物体空间中的绝对尺寸，单位为微米。平方根下的第一个平方项通常被称为“波光学项”，只要物镜的数值孔径（NA）和激发波长保持不变，这一项就保持恒定。平方根下的第二个平方项，即“几何光学项”，则取决于针孔的大小。随着针孔尺寸的增大，第二项逐渐变得显著，探测PSF的轴向分辨率几乎与针孔尺寸呈线性变化。当针孔尺寸较小时（直径小于1艾里单位，AU），探测PSF的宽度主要由公式（5.12）中的第一项决定，其近似值为

总PSF取决于激发PSF和检测PSF的相对大小。当激发PSF明显大于检测PSF时，总PSF的半最大全宽（FWHM）将主要由检测PSF决定，并随着针孔尺寸的增大而增大。相反，当激发PSF小于检测PSF时，总PSF将主要由激发PSF决定。这一点可以从图5.6中看出，图中展示了横向和轴向分辨率随针孔大小变化的关系。图中绘制的前因子分别表示横向分辨率公式（5.6）和（5.11）中 λ₀/NA_Objective 之前的系数，以及轴向分辨率公式（5.12）和（5.13）中 λ₀/（n - √(n² - NA²)） 之前的系数。随着针孔尺寸的增大，这些前因子趋于饱和。

如果针孔尺寸变得非常小（直径 ≤ 0.25 AU），则不仅公式（5.12）中的几何光学项会消失，针孔的衍射效应也会变得显著。如图5.6所示，针孔的衍射效应与激发PSF的乘积会进一步减小总轴向PSF的宽度：

Jonkman 和 Stelzer以及 Pawley用以下公式描述了共聚焦显微镜的轴向分辨率：

其中，F 是一个归一化系数，其值根据针孔的大小在1.4到2.0之间变化，也称为焦深因子。在实际应用中，共聚焦针孔通常用于控制显微镜的光学切片厚度，而不是单纯追求最高的横向分辨率。轴向分辨率通常是横向分辨率的3到4倍。

表5.1比较了两种不同类型的物镜（空气物镜和水物镜）在宽场显微镜和共聚焦显微镜中理论上可达到的分辨率。假设激发波长为500 nm，检测波长为520 nm，针孔大小为1艾里单位（AU）。对于高数值孔径（NA）物镜，轴向分辨率的提升（约1.6倍）大于横向分辨率的提升（约1.4倍）。

表 5.1

FWHM	Widefield (nm)	Confocal (nm)
NA=0.5, n=1.00
Lateral	530	374
Axial	4896	3348
NA=1.27, n=1.33
Lateral	208	147
Axial	759	480

扫描共焦成像

在共聚焦显微镜中，通过针孔的光线通常被点探测器或相机的少量像素检测到。因此，为了记录完整的图像，必须对样品进行扫描。扫描功能是共聚焦显微镜与其他光学仪器的主要区别之一，除了针孔的应用之外。根据激光与样品之间的扫描技术，共聚焦显微镜可以进行分类。下文将讨论几种最典型的扫描方法。

平台扫描

扫描样品最简单直接的方法是采用平台扫描技术。明斯基在其第一台共聚焦显微镜中成功应用了这种方法。在平台扫描过程中，光学元件保持静止，而样品在三维空间中逐点移动，每次移动到新位置后测量该点的光强。这种技术至今仍在广泛使用，尤其是在材料科学领域，其优势主要体现在以下几个方面：带有平台扫描功能的共聚焦显微镜结构简单，所需的光学元件最少，稳定性高，且对准过程简便。借助现代压电扫描仪，平台扫描可以实现极高的精度，能够在三维空间中以亚纳米级分辨率移动样品。当需要利用共聚焦显微镜的光学切片功能获取三维信息时，z方向的扫描尤其重要。

然而，平台扫描也存在一些局限性。首先，样品必须被移动，这对于生物样本来说可能是一个问题，因为生物样本通常对机械移动较为敏感。如果样品在扫描过程中发生移动，可能会导致记录的图像出现失真。此外，平台扫描使得与样品的交互变得较为困难。例如，若要使用微量移液管对样品进行操作，除非将微量移液管安装在扫描台上，否则很难实现。压电扫描仪的最大扫描速度有限，且在移动到新位置时通常需要几毫秒或更长的松弛时间。这使得压电扫描仪在需要快速精确控制样品与激光束相互作用的场景中难以应用。

激光扫描

记录共聚焦图像的第二种方法是让光束在静止的样品上进行光栅扫描。光栅扫描技术的历史甚至比共聚焦显微镜的概念还要早。然而，直到1987年，White等人首次成功地将激光扫描技术与共聚焦显微镜技术相结合。在激光扫描方法中，通常使用一对振镜，通过采集软件控制光束在x和y方向上的移动。 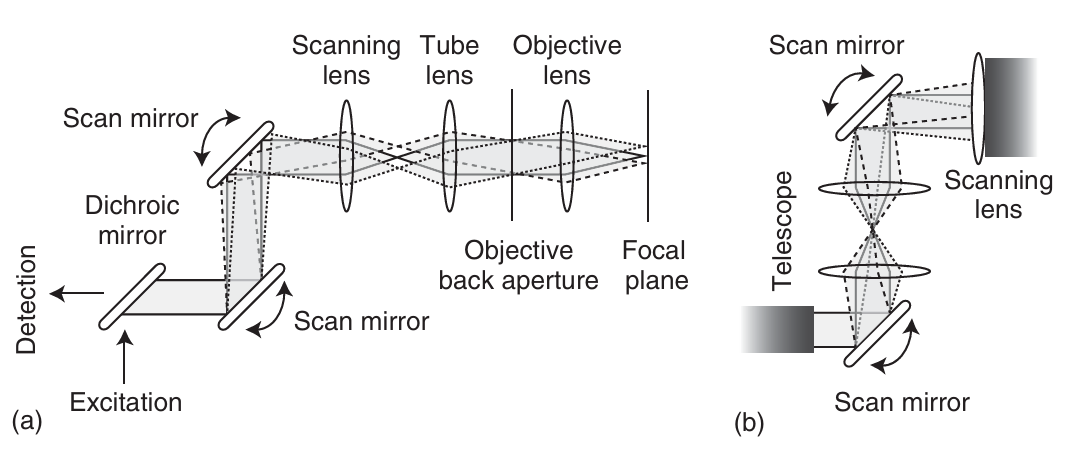图5.7展示了两种激光扫描方法。 (a) 第一种方法是将两面镜子放置得相对较近。随后，利用望远镜（通常以管透镜为其中一个关键元件）将两面镜子之间的平面成像到物镜的后焦平面上。望远镜的作用是确保在扫描过程中，激发光束不会被物镜的后孔径截断。
(b) 第二种方法更为精巧，即在两个扫描镜之间插入一个望远镜。这样，第一面镜子被成像到第二面镜子上，而第二面镜子则被成像到物镜的后焦平面上。

图5.7a展示了一种激光扫描共聚焦显微镜（LSCM）的可能配置，其中两面反射镜在垂直方向上扫描光束，且两面反射镜间距较近。为了避免物镜对光束的剪切效应，在扫描镜之后的光路中安装了一个望远镜，用于将两个反射镜之间的中间位置成像到物镜的后孔上。这意味着激发光束相对于物镜的位置保持相对固定，而光束的角度会随着反射镜的移动而变化。因此，光束在样品上的位置会随反射镜位置的变化而变化，但进入物镜后孔的光路位置是固定的。尽管图5.7a中的配置能够满足大多数成像需求，但它并非最优设计，可以通过图5.7b所示的方式进行改进。在图5.7b中，在两面镜子之间安装了一个望远镜，将第一面镜子的像投射到第二面镜子上。另一个望远镜则将第二面镜子的像投射到物镜的后孔上。经过正确对准后，激发光束在物镜的后孔处保持静止，穿过物镜，并根据两个反射镜的角度激发样品的特定位置。使用振镜扫描时，几乎可以实现视频速率的成像。如果愿意牺牲扫描速度的灵活性，可以采用共振扫描仪，从而实现更高的帧频。

然而，激光扫描也存在其代价。我们必须接受光束几乎始终偏离光轴的事实。因此，光学器件的校准变得更加重要，需要使用高质量的光学元件来尽量减少离轴球差和色差。

旋转盘共聚焦显微镜

尽管现代技术已显著提升了激光扫描共聚焦显微镜（LSCM）的性能，但在像素停留时间（以获取良好的光子统计数据）与合理的扫描速度之间，仍需找到一个理想的平衡。一般来说，图像采集速度通常在几秒到几十秒之间，具体取决于扫描仪的类型、扫描区域的大小等因素。然而，这一速度对于观察许多动态生物过程来说往往过慢，尤其是当研究者对实时动态变化感兴趣时。作为一种替代方案，可以采用旋转盘共聚焦显微镜（SDCM）。

旋转盘共聚焦显微镜（SDCM）结合了共聚焦显微镜的高分辨率成像优势和宽场显微镜的实时数据采集速率。通过在样品上同时扫描多个针孔，SDCM能够显著提高扫描速度。旋转盘扫描技术的历史可以追溯到1884年，当时德国工程师尼普科夫（Nipkow）开发了一种用于图像扫描的装置，并将其称为“电动望远镜”。其核心部件是一个带有多个小孔的圆盘（现称为尼普科夫圆盘），这些小孔呈阿基米德螺旋状排列（如图5.8所示）。当将该圆盘置于图像前方时，只有位于小孔前方的图像部分能够通过。这种孔的排列方式使得圆盘旋转一周时，图像的每个部分都能被扫描相同的时间。通过旋转圆盘，图像被转换为一系列模拟信号，随后这些信号可以通过另一个具有相同孔洞排列的圆盘重新组合成完整的图像。这种机械信号传输方式在20世纪20年代首次被用于电视广播，但由于无法与使用阴极射线管（即布劳恩管）的电子方式相媲美，尼普科夫圆盘逐渐被遗忘。直到1967年，Egger和Petran才重新认识到这种工具在共聚焦显微镜中的潜在应用价值。

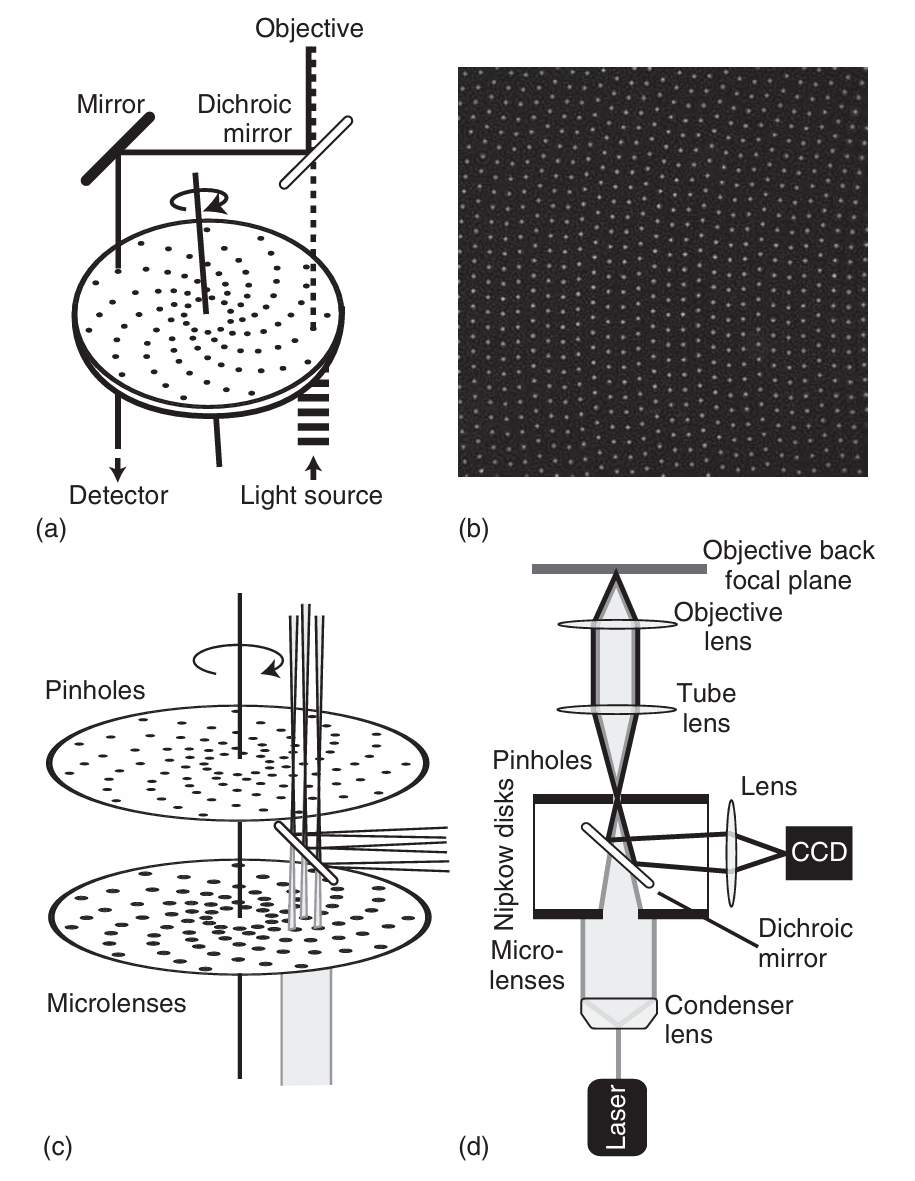
图 5.8 展示了旋转圆盘共聚焦显微镜（SDCM）的结构和原理。 (a) 为尼普科夫圆盘的示意图以及串联扫描盘显微镜的扫描头简图。这种显微镜利用同一尼普科夫圆盘的不同区域分别进行激发和检测。 (b) 展示了从一个静止的尼普科夫圆盘上拍摄的针孔结构图像。 (c) 为带有两个尼普科夫圆盘的 SDCM 设置示意图。其中一个圆盘包含针孔，另一个则装有微透镜，用于增强通过针孔的激发光强度。图中，灰色表示激发光，白色带黑边表示检测光。 (d) 为 SDCM 的激发（灰色）和检测（白色带黑边）光路的示意图。

如图5.8a所示，将带有针孔阵列的尼普科夫（Nipkow）圆盘放置在物镜的共轭像面上。与激光扫描共聚焦显微镜（LSCM）相比，这种方法能够在极短的时间内（最短1毫秒）连续扫描样品的每个点。图5.8b展示了静止的尼普科夫圆盘上针孔的结构图像。激发光束被圆盘分割成多个光束阵列，每个光束在样品中形成独立的焦点体积。

为了实现共聚焦检测并正确重组来自不同针孔的荧光信号，可以采用两种方法：一种是使用位于圆盘直径相对位置的螺旋上的共轭针孔分别进行激发和检测，如图5.8c所示（串联圆盘扫描显微镜）；另一种是使用同一组针孔同时完成激发和检测，如图5.8d所示（单面圆盘扫描显微镜）。由于后一种方法所需的维护工作较少，因此更受青睐。

由于同时测量多个探测体积，共聚焦图像的检测通常使用相机，而不是雪崩光电二极管（APD）或光电倍增管（PMT）。因此，显微镜可以从电荷耦合器件（CCD）相机的高量子效率中受益。为了正确再现图像，相机的帧频必须与尼普科夫圆盘的旋转频率同步。否则，圆盘旋转将不完全，导致图像亮度不均匀，出现条纹图案。在采集时间较短时，这一点尤为重要。

在确定尼普科夫圆盘的光学配置时，需要考虑多个参数。由于尼普科夫圆盘的设计，大量激发光会被阻挡。旋转圆盘共聚焦显微镜（SDCM）的透射系数或填充因子 T 的计算公式为

其中，D 是针孔的直径，S 是不同针孔之间的距离。与激光扫描共聚焦显微镜（LSCM）相比，旋转圆盘共聚焦显微镜（SDCM）的透射系数（T）通常要低得多。据粗略估计，大约有50%的激发光可以通过共聚焦点扫描显微镜的针孔，而基于针孔的SDCM只能达到大约5%的激发光通过针孔。可以通过减小针孔之间的间距或用狭缝孔取代共聚焦显微镜的针孔来提高透射系数。对于狭缝式共聚焦显微镜来说，

其中，D 是狭缝的宽度，其透射率通常约为10%。然而，使用狭缝形针孔或紧密间隔的孔径可能会导致针孔之间的串扰问题。这意味着，虽然来自焦外区域的光线会被相应的针孔阻挡，但它们仍可能穿过相邻的针孔，从而降低轴向分辨率（详见下文）。因此，大多数商业系统通常采用填充系数较低的针孔设计。

为了弥补激发光束吞吐量低的缺陷，通常采用由横河公司首次提出的微透镜系统。如图5.8c和d所示，横河公司设计的微透镜圆盘与尼普科夫圆盘上的针孔排列方式相同，并与之同步旋转。使用微透镜后，填充因子可提高至约40%。然而，要达到这一数值，选择最佳针孔尺寸至关重要。一方面，如果针孔直径 D 过小或孔间距 S 过大，会阻挡大量激发光；另一方面，如果针孔直径 D 过大或孔间距 S 过小，则会增加针孔串扰。因此，选择合适的孔间距 S 的目的是在最小化针孔串扰、优化扫描速度和控制样品曝光之间找到最佳平衡。

表 5.2

Advantages of the SDCM	Disadvantages of the SDCM
Faster scanning capabilities	Low transmission factors
Can be combined with higher quantum-yield detectors	Lower flexibility (e.g. fixed pinhole size)
Higher biocompatibility as a result of a reduction in excitation energy per unit area	Lower axial resolution

旋转圆盘共聚焦显微镜（SDCM）的横向分辨率与其他共聚焦成像方法相似，选择1艾里单位（AU）的针孔通常是一个理想的折中方案。然而，轴向分辨率会受到针孔串扰的显著影响，从而大幅降低显微镜的光学切片能力。对于针孔尺寸极小（约0.25 AU）的极薄样品，可以使用公式（5.15）来估算SDCM的光学切片能力，其中针孔圆盘的前置因子为0.67，狭缝孔径的前置因子为0.95。在其他情况下，公式（5.12）可用于估算探测点扩散函数（PSF），但需要注意的是，公式（5.12）和（5.15）均未考虑潜在的针孔串扰。由于针孔串扰的影响还取决于一些不可量化的参数，例如样品的标记密度，因此很难给出一个具体的轴向分辨率公式。简而言之，当荧光标记局限于薄层时，针孔串扰的影响较小；否则，焦外区域的信号可能会通过相邻针孔进入检测路径。当然，可以通过减小针孔尺寸或增大针孔间距来提高轴向分辨率，但如前所述，这将以牺牲信号强度为代价。

除了SDCM，还有多种方法可以生成和扫描样品上的多个点。其中一种方法是利用全息分束器进行双光子激发，以产生多个激发光束；或者在适当的共轭像平面上扫描二维（2D）针孔阵列，而不是使用圆盘。尽管这些方法在所有情况下都能提高扫描速度，但这种提升往往需要做出一定的妥协（详见表5.2）。然而，正如明斯基对实时成像的重视所表明的那样，SDCM及其类似方法已成为极具价值的工具，因为它们结合了共聚焦显微镜的高对比度成像优势和宽场显微镜的快速数据采集能力。通过同时使用多个针孔进行扫描，激发功率在空间和时间上更加均匀地分布在样品上，从而降低了单位面积的激发功率。因此，与激光扫描共聚焦显微镜（LSCM）相比，SDCM具有更高的生物相容性。

共聚焦去卷积

尽管共聚焦显微镜图像的对比度有所提高，但其分辨率仍受到衍射的限制。为了突破这种衍射限制，可以采用超分辨率显微镜技术。此外，还可以通过去卷积技术来提高共聚焦图像的分辨率。共聚焦显微镜的光学分辨率降低主要是由于实际图像与显微镜的衍射极限点扩散函数（PSF）发生卷积所致。从数学角度来看，空间坐标 r 处的检测信号 S(r) 是由原始物体的信号 O(r) 与点扩散函数 PSF(r) 卷积得到的：

当已知两个函数（例如观测信号 S(r) 和点扩散函数 PSF(r)）时，理论上可以推导出第三个函数（在本例中为物体的实际空间分布 O(r)）。然而，在实际应用中，噪声或对已知函数信息的有限了解可能会使去卷积过程变得复杂，甚至无法实现。

因此，无法直接通过公式（5.19）获得 O(r)，而必须借助更复杂的去卷积算法。图5.9展示了一个正在进行有丝分裂且微管蛋白被标记的细胞图像。与宽场图像（图5.9a）相比，共聚焦图像（图5.9b）的对比度显著提高。而在经过去卷积处理的图像（图5.9c）中，纺锤体的完整结构得到了更清晰的解析，对比度进一步提升。

一种著名的去卷积方法是Richardson-Lucy算法，图5.9中的去卷积处理便采用了该算法。图像中检测到的信号不仅取决于物体信号的原始分布，还与通过系统点扩散函数（PSF）传播至相应像素的概率有关。当 u_kl 表示来自像素 (k, l) 的光强，PSF_ij;kl 表示来自位置 (k, l) 的光在位置 (i, j) 被检测到的概率时，像素 (i, j) 中检测到的信号可以表示为

当 u_kl 服从泊松分布，即主要噪声源为光子噪声时，如果公式（5.20）中的所有其他参数均已知，那么可以在迭代步骤 t + 1 中反复计算 u^(t+1)_kl 的最可能值：

事实证明，当这些迭代收敛时，结果将是 u_kl 的最大似然估计值。为了进行更精确的去卷积，需要对点扩散函数（PSF）有详细的了解。例如，仔细观察图 5.9c 的左下角可以发现，由于物镜的畸变，该区域的 PSF 可能发生了变化。因此，在图像的这一部分，去卷积可能无法得出 u_kl 的正确值。然而，即使在不知道 PSF 的情况下，仍可以通过盲去卷积技术来提高图像质量。

共聚焦显微镜的应用

在生物科学领域，共聚焦显微镜的主要应用是成像。使用共聚焦显微镜记录多色三维图像已成为一种常规操作。图5.10展示了一个使用旋转圆盘共聚焦显微镜（SDCM）记录的三维共聚焦图像示例，该示例也提供在在线资料中。在图中，HMEC-1细胞的质膜被标记为红色，而线粒体被标记为绿色。线粒体复杂的三维网络结构在整个细胞中清晰可见。此外，通过膜标记物内化标记的早期内体也可通过测量信号的位置和形态与质膜区分开来。

尽管成像是共聚焦显微镜最常见的应用，但在生化和生物物理科学中，共聚焦显微镜还有许多超出成像范围的重要应用。在后续章节中，我们将讨论一些利用共聚焦显微镜的荧光波动光谱技术。

非扫描应用

荧光相关光谱学

荧光相关光谱（FCS）是一种从荧光强度波动中提取信息的多功能技术，相关文献中已有诸多详细的论文和综述。FCS最早由Magde、Elson和Webb在20世纪70年代初提出 。该方法通过相关分析处理荧光强度的时间波动，从而获取有关波动过程的信息。随着超灵敏探测器和稳定激光光源的发展，利用较小的共聚焦检测体积（1~1飞升）检测单个荧光团信号成为可能 。这种灵敏度的提升使得FCS能够广泛应用于多个领域。

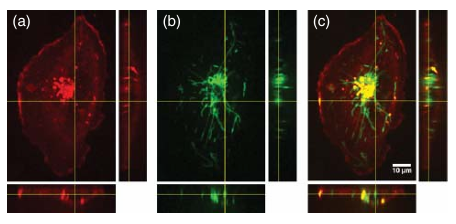
图5.10 三维（3D）共聚焦成像。 图中展示了一个HMEC-1细胞的图像，其中不同的细胞器用不同的颜色标记。（a）显示使用CellMask™（深红色，Life Technologies）标记细胞膜的x-y、x-z和y-z平面的三维图像切片（红色）；（b）显示使用MitoTracker®（GreenFM，Life Technologies）标记线粒体的x-y、x-z和y-z平面的三维图像切片（绿色）。（c）显示合并图像，其中由内化的膜标记物指示的早期内体显示为黄色。 借助共聚焦显微镜改进的3D分辨率，可以清楚地区分质膜、线粒体网络和内体的各种结构。

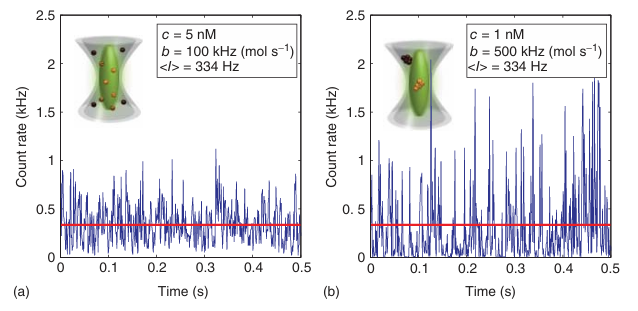图5.11 低浓度下的荧光强度波动。(a) 模拟浓度为5nM，分子亮度（b）在PSF中心为每分子100kHz的分子样本。(b) 模拟浓度为1nM，分子亮度在PSF中心为每颗粒500kHz的样本。两种情况下，平均强度⟨I⟩ 均相等。

图5.11展示了两种不同浓度和分子亮度的物质在溶液中自由扩散时的荧光强度随时间变化的轨迹。尽管这两种样品的平均荧光强度相同（用实线表示），但它们的荧光强度波动却大不相同——浓度较低但亮度较高的物质表现出更大的波动。这种荧光强度的变化源于布朗运动导致的共聚焦检测体积内粒子数量的热力学波动。通过分析荧光强度的时间波动，可以提取有关体积内粒子平均数量以及粒子通过共聚焦体积所需的平均时间的信息。当共聚焦体积的形状和大小已知时，可以将分子的平均数量及其在共聚焦体积中停留的时间转换为平均浓度和平移扩散系数。

FCS的应用范围不仅限于扩散过程。任何导致荧光强度波动的过程都可以通过FCS进行分析。因此，即使在平衡状态下进行测量，也可以通过FCS测量单重态-三重态动态过程和化学反应速率（当反应导致分子亮度变化时）等。

为了从荧光信号波动中提取信息，我们采用相关分析方法。来自同一分子的光子会产生相关信号，而来自非相关过程的随机光子则不会产生相关信号。相关分析具有高度灵敏性，可用于确定两个信号保持相似的时间尺度，或者在自相关分析中，确定单个信号的波动平均持续多长时间。以分子在共聚焦体积内扩散为例，荧光信号会随着分子进出焦点而波动。波动的平均时间尺度取决于分子穿过共聚焦点所需的时间，称为扩散时间 τ_D。τ_D 取决于共聚焦体积的大小和分子的扩散系数 D。在小于或等于 τ_D 的时间尺度上，分子在体积内的位置变化不大，检测到的信号保持相似。而在更长的时间尺度上，分子可以进入或离开共聚焦体积，荧光信号发生变化，相关性下降。因此，当时间超过 τ_D 时，相关函数会显著衰减。

关于FCS的自相关推导，可参考Elson和Magde的工作。对于在三维空间中自由扩散的分子，某一时间 t 的荧光信号 F(t) 的强度为

其中，ε 是分子亮度，C(r, t) 是在时间 t 时，位置 r 处的分子数量密度，W(r) 是归一化的点扩散函数（PSF），定义为 W(r)/W(0)，其中 W(0) 是PSF中心的激光强度。分子亮度 ε 被定义为在PSF中心处，单个荧光团的荧光强度，其值为

其中，κ 是显微镜的总检测效率，σ_Abs 是荧光团在激光波长处的吸收截面，ϕ 是荧光团的荧光量子产率。自相关函数（ACF）可以表示为

其中，⟨ ⟩ 表示时间平均值。自相关函数（ACF）的计算过程如图5.12所示。在相关分析中，信号以时间间隔 τ 进行移位，与原始信号相乘，并在整个荧光时间轨迹上进行积分。最终，将相关分析的结果除以平均荧光强度的平方，并减去1，以完成归一化处理。

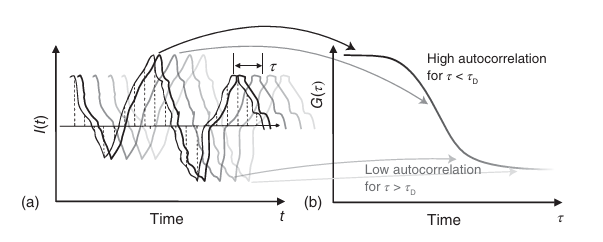
图 5.12 自相关函数的确定。(a) 荧光信号的示意图（黑色曲线）围绕平均值（黑色水平线）波动；(b) 由此产生的自相关函数。轨迹被复制并以不同的时间延迟 𝜏 移动（不同的灰度值）。移动后的曲线与原始曲线相乘并积分，以确定信号的残余自相似性。相似性从黑色衰减到浅灰色，可以从相关幅度的下降中看出。

共聚焦显微镜的 PSF 可近似为三维高斯：

其中，w_r 和 w_z 分别表示点扩散函数（PSF）从中心到强度在横向和轴向下降至 1/e² 时的尺寸。将公式（5.22）和（5.25）代入公式（5.24），我们便得到了自由扩散粒子自相关函数（ACF）的解析表达式：

其中，⟨N⟩ 是共聚焦体积中粒子的平均数量，𝛾_FCS 是一个几何系数，取决于共聚焦体积的形状（对于三维高斯分布的点扩散函数，𝛾_FCS = 2^3/2），而 𝜏_D = 𝜏_2r/4D 是扩散时间。

也可以将 ACF 定义为

公式（5.27）所示的自相关函数（ACF）表达式与在时间 t = 0 时检测到一个光子，而在延迟时间 𝜏 检测到另一个光子的概率成正比。在时间尺度远小于扩散时间 𝜏_D 的情况下，分子仍然留在共聚焦体积内，因此检测到第二个光子的概率较高。而在较长的时间尺度上，由于粒子可能通过布朗运动离开共聚焦体积，检测到第二个光子的概率会降低。相关分析的强大之处在于它能够检测荧光强度中任何类型的非随机波动。图5.13举例说明了可以使用荧光相关光谱（FCS）检测的过程。

⚠️upload failed, check dev console

图 5.13：水溶液中绿色荧光蛋白 (GFP) 的测量自相关函数 (ACF)。 通过 FCS 可以检测到许多过程，并在 ACF 中突出显示：(a) 反聚束现象，其出现是由于荧光团在发射第二个光子之前必须重新激发（为了检测反聚束现象，需要两个检测器来避免检测器和数据采集卡的死时间），(b) 旋转扩散，(c) 分子内反应，例如单线态到三线态之间的跃迁，以及 (d) 平动扩散。

完整的自相关函数不仅包括由扩散引起的项，还可能包括由光子反束、分子旋转运动以及荧光分子进入和离开三重态时的闪烁引起的项。幸运的是，这些效应发生在不同的时间尺度上，因此可以通过分析将其区分开来。虽然FCS分析的是荧光强度的时间行为，但也有其他方法可以利用荧光强度的幅度来获取有关分子平均数量及其亮度的信息，例如光子计数直方图（PCH）分析、荧光强度分布分析（FIDA）和累积分析。关于这些不同亮度分析方法的详细介绍，可以参考Macdonald等人的文章。

自相关函数的振幅与共聚焦体积中的颗粒数量成反比。对于单一物种，自相关函数的振幅与分子亮度无关，而信噪比则取决于分子亮度，但与样品浓度无关，至少在FCS最敏感的浓度范围内（从约100 pM到约100 nM）是如此。

荧光交叉相关光谱学

除了自相关分析外，还可以将两个信号进行相互关联，这种方法称为交叉相关。通常情况下，使用两个对不同波长敏感的检测通道，然后对这两个通道的荧光信号进行交叉相关分析。这种双色荧光交叉相关光谱（FCCS）方法非常适合用于研究分子间的相互作用 。例如，图5.14展示了用Atto532标记一条链、用Atto647标记第二条链的双链DNA的自相关和交叉相关曲线。由于DNA的双标记效率很高，DNA分子进入共聚焦体积时，绿色通道的波动将与红色通道信号的增加相关，因此预计会表现出很强的交叉相关性。

从交叉相关函数（CCF）的振幅中，可以提取出两个通道中可检测到的双标记分子的数量 N₁₂。假设两个共聚焦体积为重叠的三维高斯分布且系统无串扰，则交叉相关函数的表达式为

其中，𝛾_FCS 是一个几何系数，当点扩散函数（PSF）采用三维高斯近似时，该系数等于 2^3/2；N_i 是第 i 类分子的数量（这里的 i 可以是通道1或通道2中可见的单标记分子，也可以是双标记分子）；𝜏_D = 𝜏_2r/4D₁₂ 是双标记分子的扩散时间，其中 D₁₂ 是双标记物种的扩散系数。

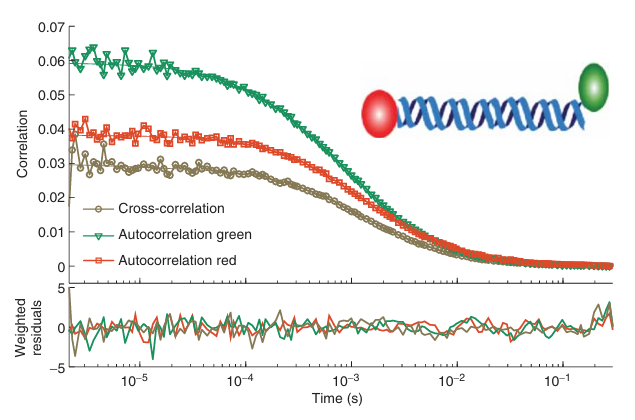
图 5.14 双标记 DNA 的互相关函数。双链 60bp DNA 在末端用 Atto532 和 Atto647 标记。图中显示了 Atto532（绿色）、Atto647（红色）的自相关函数以及相应的互相关函数（金色）。拟合曲线以相应颜色的实线表示，加权残差绘制在下面的面板中。

虽然交叉相关函数（CCF）通常被用作判断两个分子是否相互作用的直接依据，但CCF的振幅及其相对于自相关函数的相对高度实际上包含了携带两种荧光团的复合物的百分比信息。Foo等人 详细介绍了如何对双色荧光交叉相关光谱（FCCS）数据，特别是荧光蛋白数据进行定量分析。

脉冲交织激励

使用脉冲间交替激发（Pulsed Interleaved Excitation, PIE）可以进一步提高双色荧光交叉相关光谱（FCCS）的灵敏度。PIE是由Shimon Weiss实验室开发的一种基于双交替激光激发（ALEX）的技术，其核心改进在于使用亚纳秒脉冲激光进行激发，并在纳秒时间尺度上交替（或交错）使用。为此，激发激光需要同步并相互延迟12-20纳秒（约为所用染料荧光寿命的4-5倍）。在检测时，可以使用与激发激光同步的计时器记录光子，从而将每个检测到的光子分配给其对应的激发源（见图5.15a）。在数据收集方面，一种更先进的方法是使用时间分辨单光子计数（TCSPC）检测。TCSPC的另一个优点是可以生成并分析荧光团的寿命直方图。通过寿命信息，可以确定是否存在淬灭现象，例如由于Förster共振能量转移导致的淬灭。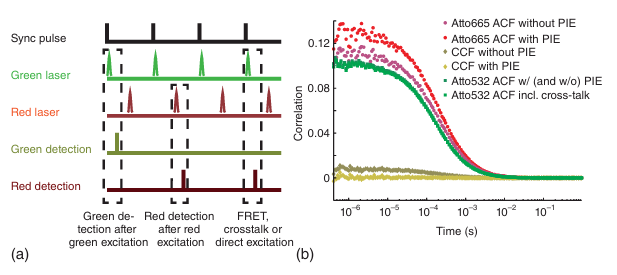

图 5.15 脉冲交错激发 (PIE)。(a) 一个展示 PIE 原理的示意图。(b) 使用和不使用 PIE 测得的在溶液中自由扩散的 Atto532 和 Atto665 的自相关函数 (ACF) 和互相关函数 (CCF)。 可以观察到串扰和直接激发对红色 ACF 和 CCF 的影响，而这些影响在使用 PIE 时会被完全消除。

图5.15b展示了溶液中未发生相互作用的荧光团的自相关函数（ACFs）和交叉相关函数（CCFs）。由于相关光谱法对相关事件非常敏感，Atto532荧光团与Atto665通道之间的交叉干扰信号在CCF中产生了残余的交叉相关振幅。这种光谱串扰源于红色通道检测到的绿色荧光团的荧光发射光谱的尾部。如果不大幅降低系统对红色荧光团的灵敏度，仅使用适当的发射滤光片是无法完全抑制红色通道中的光谱串扰的。光谱串扰不仅会影响CCF的振幅，还会影响红色ACF的振幅，因为绿色荧光团在红色检测通道中充当了第二种荧光团。使用PIE时，可以将绿色激发后在绿色通道检测到的光子与红色激发后在红色通道检测到的光子进行交叉相关，从而完全避免光谱串扰（见图5.15b中的淡金色数据）。如果在绿色通道中选择适当的发射滤光片，红色荧光团的荧光就不会出现在绿色通道中。此外，只要选择正确的红色激发波长，就可以避免绿色荧光团受到激发。因此，PIE CCF是无串扰的。此外，在红色激发后，根据红色通道检测到的光子确定的ACF也没有光谱串扰。使用PIE时，红色ACF的振幅增大（见图5.15b中的红色数据），这表明去除光谱串扰后，红色ACF的振幅得到了定量上的正确反映。绿色ACF的振幅不受PIE的影响（见图5.15b中的浅绿色数据）。将串扰光子重新分配到正确的检测通道会提高检测到的分子亮度，当绿色激光（530纳米）直接激发红色染料（此处为Atto665）的亮度可以忽略不计时，这一点尤为明显。分子亮度的增加将提高ACF的信噪比，但在只有单一扩散物种存在时，不会改变函数的形状或振幅。

这一FCCS的改进对于生物样本中分子相互作用的研究至关重要，因为PIE能够区分相关生物分子的微弱相互作用与完全没有相互作用的情况。由于PIE记录了每个光子的检测通道和激发源，因此可以在事实上定义不同的通道，并将“错位”的光子重新分配到正确的通道。例如，将绿色激发后检测到的所有光子与红色激发后检测到的光子进行交叉相关，就能得到CCF，即使在存在FRET的情况下也能进行定量评估。

利用多参数荧光检测进行脉冲串分析

共聚焦显微镜具有较小的探测体积，能够检测稀释样品中的单个分子 。当单个荧光分子扩散通过显微镜焦点时，会产生光子猝发。从单个分子的猝发中收集到的所有光子会被累积并分析。为了从每个光子中提取尽可能多的信息，采用了多参数荧光检测（MFD）技术（示意图见图5.16）。在MFD中，首先使用偏振分光器将荧光发射信号分为平行和垂直两种偏振方向，然后通过二向色分光器将这两种偏振通道分开，从而在光谱上分离光子。

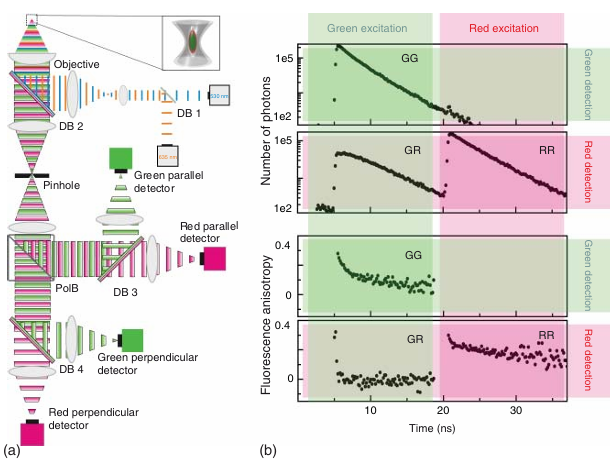
图 5.16 采用脉冲交错激发的多参数荧光检测。(a) 多参数荧光检测-脉冲交错激发 (MFD-PIE) 装置的示意图。(b) 使用 MFD-PIE 记录的双标记 DnaK（一种细菌热休克蛋白 70）的实验数据。MFD-PIE 能够根据光子的光谱范围、偏振态和激发光源对光子进行分离。与 PIE 技术一样，激发光源的分配依据检测到的光子相对于同步脉冲的到达时间。通过 MFD-PIE 测量，可以确定各种通道的化学计量比、荧光寿命（上图）或时间分辨各向异性（下图）。

根据MFD数据，可以确定不同通道的荧光寿命 𝜏 和各向异性 r（见图5.16b）、每个物种的分子亮度 𝜂、每个通道的荧光强度，以及每个光子相对于测量开始的到达时间（时间分辨率可达100纳秒或更高）。如图5.17所示，脉冲间交替激发（PIE）可以与MFD结合使用，为测量提供化学计量学信息 。

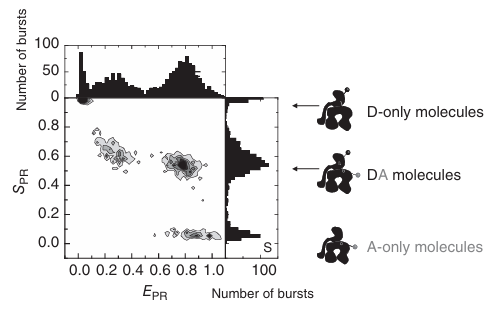
图 5.17：双标记 DnaK 分子的 FRET 效率与化学计量比关系图。 通过化学计量比数值，可以将只含供体和只含受体的分子从双标记分子或复合物中分离出来。 因此，可以确定不受只含供体分子污染的单分子 FRET 直方图。

MFD具备双色检测功能，非常适合用于单分子佛斯特共振能量转移（spFRET）实验。当两个荧光团附着在单个分子或复合物上且它们之间的距离在100 Å以内时，会发生FRET。通过测量两个通道的相对强度，可以确定FRET效率以及两个荧光团之间的距离。因此，可以推断蛋白质和其他生物相关分子的结构特征，并测量其在细胞内的动态变化，空间分辨率可达几微米。在使用MFD进行的spFRET测量中，每个猝发的FRET效率通常是根据转移光子数（I_FRET）与猝发中光子总数（I_FRET + I_Donor）的比值来确定的：

其中，𝛾 表示供体通道 (D) 和受体通道 (A) 的不同检测效率，这可以在不同的实验中确定，或者根据荧光团各自的量子产率𝜙 和不同检测途径的效率𝜂 计算得出：

计算出的单个分子的 FRET 值通常会绘制成一维直方图。使用 PIE 时，还可以确定每个猝灭的化学计量。化学计量描述的是绿色激发后收集到的光子与检测到的总光子之比：

其中，I_Acceptor 是在红色激发后在受体通道中收集到的光子数。图5.17展示了细菌热休克蛋白70（DnaK）的FRET效率与化学计量比的二维直方图。通过化学计量值（公式（5.31）），可以轻松区分仅用单个供体或受体荧光团标记的蛋白质与双标记分子。从FRET效率与化学计量比的直方图中，可以选择来自双标记分子的猝发事件，并利用多参数荧光检测（MFD）提供的数据进行进一步分析。从猝发分析实验中可以提取出有关动态过程、亚群信息以及分子间距离等详细信息，这一点令人印象深刻。

猝发分析实验的主要限制因素是收集到的光子数量和实验的信噪比。因此，共聚焦显微镜的小探测体积和高灵敏度在推进基于溶液的单分子方法中发挥了重要作用。

扫描应用超越成像

除了上述方法外，还有许多其他技术可用于分析荧光信号波动中的信息。其中许多方法同样适用于通过共聚焦显微镜收集的图像数据。在此，我们重点介绍两种方法：数量与亮度（N&B）分析和光栅图像相关光谱法（RICS）。

数量和亮度分析

图5.11展示了粒子数和分子亮度对平均强度和方差的影响。实验模拟了两种溶液A和B，其中A的分子亮度比B低5倍，但A的浓度是B的5倍。尽管两种溶液的平均亮度 ⟨I⟩ 相同，但溶液B的荧光强度波动（图5.11b）——因此方差 σ²——明显大于溶液A（图5.11a）。数量与亮度（N&B）分析法 [35] 是分析荧光强度轨迹或一系列荧光图像波动的最直接方法。N&B分析基于两个假设：一是检测体积内只存在一种具有特定亮度的物种；二是检测到的平均荧光强度 ⟨I⟩ 与检测体积内的分子数 n 和荧光物种的表观亮度 b 成正比：

其中，b 表示单位时间内每个分子发射的光子数。荧光信号的方差由两部分组成：一是检测体积内荧光分子数量的波动引起的方差（σ²_颗粒），二是光子噪声引起的方差。由于荧光分子数量的波动遵循泊松分布，其分布的方差等于平均值，因此检测体积中粒子数量的方差等于分子的平均数量 ⟨n⟩。此外，由分子数量波动引起的荧光信号方差（σ²_颗粒）与分子亮度的平方成正比：

光斑噪声来源于荧光发射并非稳定发生，而是遵循泊松概率分布：

其中，k 是出现的次数，𝜆是出现的平均次数（如发射的光子）。因此，光斑噪声的方差由平均强度给出，𝜎2 光斑噪声 = ⟨I⟩。信号的总方差是两个过程的总和：

将射噪修正纳入公式 (5.32) 和 (5.33) 得到

为了从任意时间间隔内发射的光子数中提取更具物理意义的特性，我们引入了分子亮度 𝜀 。分子亮度被定义为当荧光团位于点扩散函数（PSF）中心时，每个分子每秒被检测到的光子数。表观亮度 b 与分子亮度 𝜀 之间通过荧光轨迹的时间分段 T_bin 呈线性关系：

需要注意的是，同一荧光团的分子亮度在使用不同设备测量时可能会有所不同，因为它取决于共聚焦光斑中每秒的激光光子数 W(0) 和整个系统的检测效率 𝜅（见公式（5.23））。

N&B方法提供了一种直接分析给定强度轨迹或图像序列中单个像素波动的手段。由于N&B方法假设检测体积内只存在单一物种，并且不对点扩散函数（PSF）的形状进行任何假设，因此其精度不如其他基于亮度的方法（如光子计数直方图分析PCH或荧光强度分布分析FIDA）。然而，这种方法计算简便快捷，通常能够提供足够的信息。图5.18展示了N&B分析的一个实例。

图5.18a显示了DNA甲基转移酶1在缓冲液中的荧光强度随时间的变化。整体荧光强度随时间逐渐衰减。通过N&B分析（见图5.18b），我们发现颗粒数量随时间减少，而分子亮度保持不变。这表明DNA甲基转移酶1的浓度由于蛋白质吸附在样品架表面而不断降低。

图5.18c展示了溶液中Atto532样品的荧光强度，测量过程中激光功率逐步增加。随着激光功率的增加，分子亮度也在增加（见公式（5.22））。这反映在N&B分析中，亮度随激光功率的增加而增加，而分子数量保持不变（见图5.18d）。

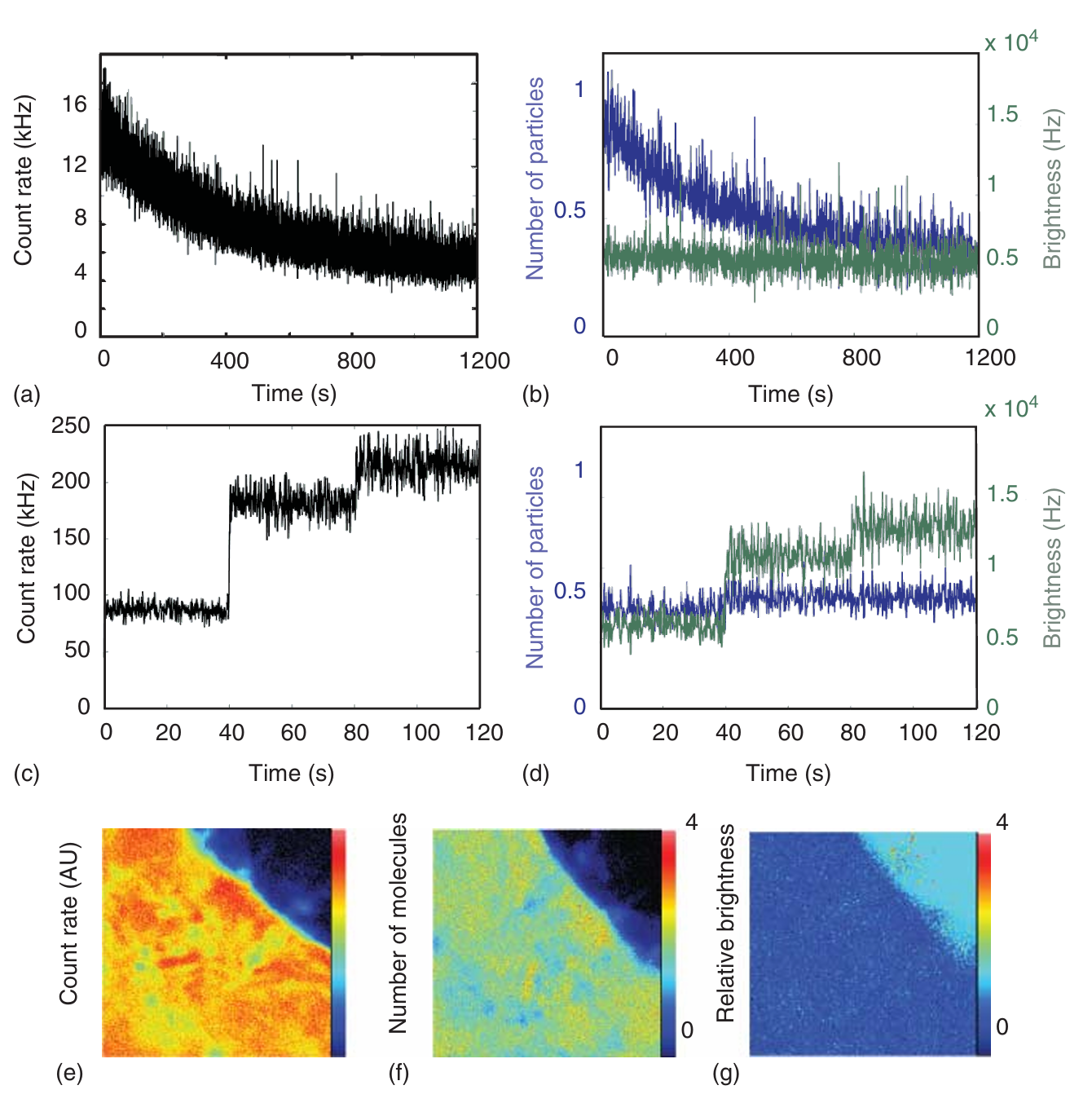
图5.18展示了两种不同测量结果的荧光强度轨迹（黑色）以及相应的N&B分析（数量为蓝色，亮度为绿色）。 (a) 溶液中DNA甲基转移酶1（Dnmt1）的测量结果。荧光强度随时间变化。 (b) 使用滑动窗口对图(a)中的强度轨迹进行N&B分析。结果显示，分子数量（蓝色）随时间减少，而分子亮度（绿色）保持不变。这表明随着越来越多的分子吸附到样品室表面，溶液中的分子数量减少，而分子亮度不受影响。 (c) 溶液中Atto532的荧光强度。在测量过程中，激光功率逐步增加。 (d) 使用滑动窗口对图(c)中的强度轨迹进行N&B分析。分析结果显示，分子亮度（绿色）随着激光功率的增加而逐步提高，而分子数量（蓝色）保持不变。 (e) HeLa细胞中细胞质GFP的荧光测量。图中展示了图像序列中的代表性图像，其中高计数率区域清晰可见。 (f) 使用N&B分析法确定的图像中每个像素的分子数量。 (g) 使用N&B分析法确定的图像中每个像素的分子亮度。

N&B分析的一个显著优势在于它可以应用于动态图像序列（如时间序列图像）。图5.18e展示了来自表达绿色荧光蛋白（GFP）的HeLa细胞的平均荧光强度。从图中可以观察到荧光强度的变化。通过对图像的每个像素进行N&B分析（见图5.18f和g），可以清晰地看到细胞质中蛋白质浓度的变化，而分子亮度保持不变。尽管对于GFP本身而言，这一结果可能看似微不足道，但它却有力地证明了该方法的有效性。当GFP与其他蛋白质融合时，N&B分析能够帮助研究人员深入了解蛋白质或复合物的寡聚态和化学计量比。

光栅图像相关光谱学

RICS（光栅图像相关光谱法） 结合了激光扫描共聚焦显微镜（LSCM）和相关光谱学的技术优势。在活细胞中进行点FCS（荧光相关光谱）测量时，光漂白是一个常见的问题，这主要是因为生物分子在细胞的拥挤环境中扩散缓慢。为了减少光漂白，可以通过扫描激光束来加快测量速度。一种方法是像扫描FCS那样进行圆形扫描，或者像RICS那样对样品进行光栅扫描（图5.19a）。在光栅扫描图像中，像素的空间间隔与测量像素之间的时间延迟之间存在一定的关系。

与FCS类似，RICS也是对荧光强度的波动进行分析。然而，在RICS中，时间信息被编码在图像内的空间信息中，并通过图像相关光谱进行分析。由于激发光束和检测光束是相对于样品移动的，这种方法可以在收集更多统计数据的同时，最大限度地减少样品每个位置对激光的暴露时间，从而有效减少光漂白。

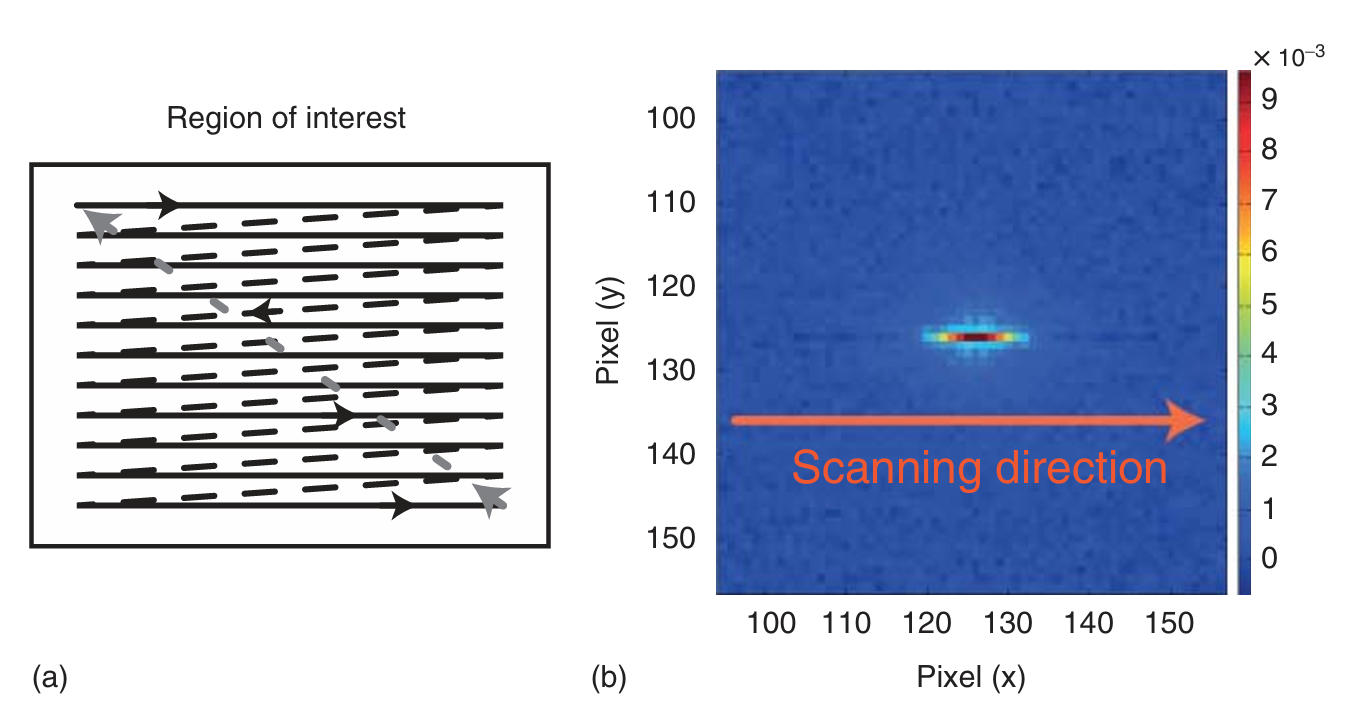
图 5.19 光栅图像相关光谱（RICS）。(a) 使用激光扫描共聚焦显微镜进行光栅扫描成像的原理。按时间线性扫描一条线，然后将光束转向下一条线的起点，再按时间线性扫描下一条线。(b) 在溶液中扩散的标记 DNA 的 50 幅系列图像（总长度为 50μm）的 RICS 相关函数，每帧记录时间为 500ms。

二维相关模式提供了沿各自轴线的扩散过程信息，而这些轴线是以不同的时间尺度进行扫描的。在x轴上，两个相邻像素的测量是连续进行的，时间延迟由像素时钟决定；而在y轴上，相邻行的两个像素之间的测量间隔则由扫描一条线所需的时间决定。在自由布朗扩散的情况下，假设为单光子激发且点扩散函数（PSF）为三维高斯分布（公式（5.25）），RICS的自相关函数（ACF）可以表示为：

在公式（5.39）中，⟨N⟩ 表示点扩散函数（PSF）内荧光分子的平均数量，D 是分子的扩散系数，𝜏_x 和 𝜏_y 分别是 x 轴和 y 轴的像素采样时间，𝜉 和 𝜓 分别是以像素为单位的 x 和 y 方向的空间滞后，s 是连续像素之间的距离。

图5.19b展示了用Atto565标记的DNA在缓冲溶液中自由扩散的RICS自相关函数（ACF）。在这里，两种不同的时间尺度变得尤为明显：沿x轴，激光扫描速度很快，除非分子的扩散速度超过激光扫描速度，否则PSF的宽度会保持不变。沿y轴，激光束需要更长的时间才能返回到同一区域。对于快速扩散的分子，短距离内的相关振幅较低，因为它们在短时间内会扩散到更远的位置；而对于缓慢扩散的分子，短距离内的相关振幅较高，但当距离超过PSF时，相关振幅会迅速衰减至零。对于固定不动的分子，其尺寸远小于PSF时，RICS返回的将是PSF的形状。

通过将RICS数据与ACF的理论表达式（公式（5.39））进行拟合，可以确定PSF内的扩散系数和颗粒的平均数量。此外，通过使用双色RICS，还可以利用交叉相关光谱来测量分子间的相互作用。图5.20展示了两种不发生相互作用的荧光团Atto488（图5.20a）和Atto565（图5.20b）在溶液中的RICS自相关函数（ACF）和交叉相关函数（CCF）。图5.20c展示了未根据脉冲间交替激发（PIE）分离光子的RICS交叉相关函数。由于Atto488的荧光进入Atto565通道的光谱串扰，即使分子之间没有相互作用，也会导致残余相关性。然而，如图5.20d所示，当考虑PIE信息，并将绿色激发后在绿色通道检测到的光子与红色激发后在红色通道检测到的光子相关联时，残余交叉相关性完全消失。因此，与荧光交叉相关光谱（FCCS）类似，PIE显著提高了双色RICS实验的灵敏度。

为了进一步提高RICS在细胞测量中的适用性，任意区域RICS算法（ARICS）对传统ICS算法进行了改进。改进后的算法可以对任意形状的感兴趣区域（ROI）执行RICS分析，这些ROI可以手动选择，也可以通过阈值自动选择，甚至可以根据第二个通道测量的参数进行选择。因此，ARICS能够测量亚细胞区域内的扩散运动。

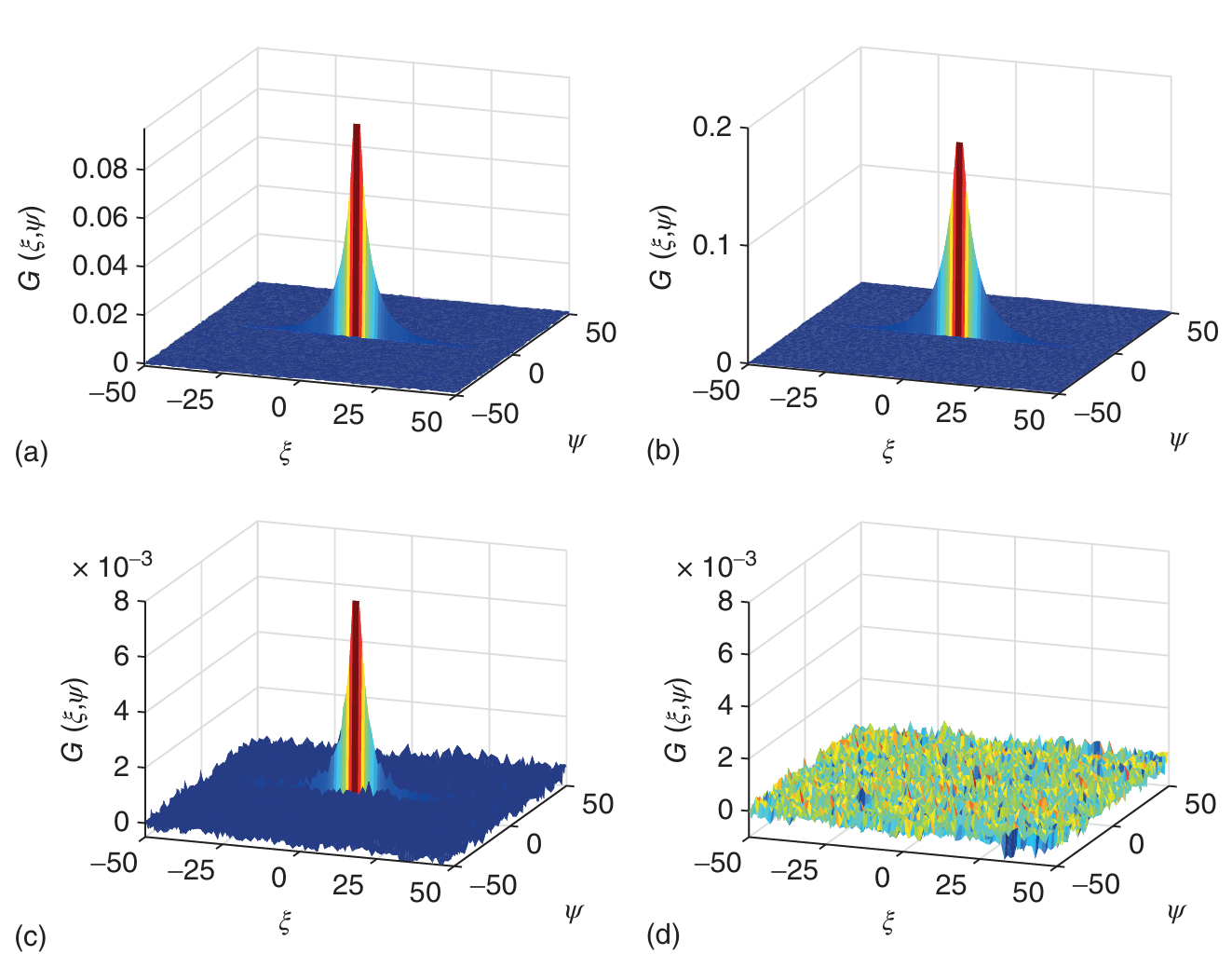
图 5.20 PIE 对交叉相关 RICS 的影响：收集了 Atto488 和 Atto565 溶液的光栅扫描图像。(c) 交叉相关函数显示的是，PIE 提供的信息未被纳入，绿色通道检测到的所有光子与其他通道检测到的所有光子相关。(d) 类似的分析，但这次利用了 PIE 信息来消除串扰。在这里，绿色激发后在绿色通道中检测到的光子与红色激发后在红色通道中检测到的光子是相关的。